题目内容
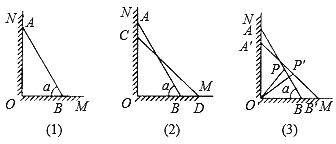
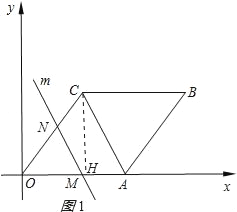
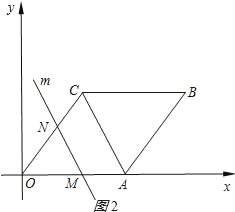
【题目】如图在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(3,4),平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与菱形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).

(1)求点B的坐标;
(2)当MN=![]() AC时,求t的值;
AC时,求t的值;
(3)设△OMN的面积为S,求S与t的函数表达式,并确定S的最大值.
【答案】(1)点B的坐标为(8,4);(2)![]() 或
或![]() ;(3)
;(3)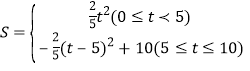 ;当t=5时,S最大值=10.
;当t=5时,S最大值=10.
【解析】
(1)过点C作CH⊥OA于H,由勾股定理求出OC,得出CB,即可得出结果;
(2)分两种情况:①当0≤t≤5时,由菱形的性质得出OA=AB=BC=OC=5,OC∥AB.由平行线得出△OMN∽△OAC,得出比例式求出OM即可;
②当5≤t≤10时,设直线MN与OA交于点E.同①可得AM=![]() .再证出△AEM∽△OAC.得出对应边成比例求出AM=AE,得出OE即可;
.再证出△AEM∽△OAC.得出对应边成比例求出AM=AE,得出OE即可;
(3)分两种情况①当0≤t<5时,求出△OAC的面积,再由相似三角形的性质得出![]() ,即可得出结果;
,即可得出结果;
②当5≤t≤10时,过点M作MT⊥x轴于T,由△BMN∽△AME可知,MT=![]() (t﹣5),得出S△OMN=S△ONE﹣S△OME=
(t﹣5),得出S△OMN=S△ONE﹣S△OME=![]() 即可得出结果.
即可得出结果.
解:(1)过点C作CH⊥OA于H,如图1所示:
∵C (3,4),
∴CH=4,OH=3,
∴![]()
∵四边形OABC是菱形,
∴CB=OC=5,5+3=8,
∴点B的坐标为(8,4);
(2)分两种情况:
①当0≤t≤5时,
如图2所示:
∵四边形OABC是菱形,
∴OA=AB=BC=OC=5,OC∥AB.
∵MN∥AC,
∴△OMN∽△OAC,
∴![]()
∵![]()
![]()
∴![]()
∴![]()
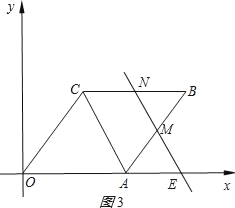
②当5≤t≤10时,如图3所示:
设直线MN与OA交于点E.,同①可得AM=![]() .
.
∵OC∥AB,MN∥AC,
∴∠COA=∠MAE,∠CAO=∠MEA,
∴△AEM∽△OAC.
∴![]()
∵OC=OA,
∴AM=AE,
∴![]()
∴![]()
综上所述:![]() 或
或![]()
(3)分两种情况:
①当0≤t<5时(如图1),![]()
∵△OMN∽△OAC,
∴![]() ,即
,即![]()
∴![]() (0≤t<5);
(0≤t<5);
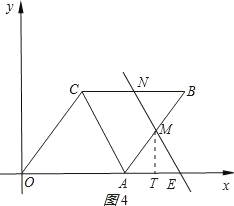
②当5≤t≤10时,过点M作MT⊥x轴于T,如图4所示:
由△BMN∽△AME可知,MT=![]() (t﹣5),
(t﹣5),
∴S△OMN=S△ONE﹣S△OME=![]()
综上所述: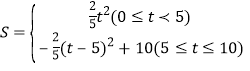
∴当t=5时,S最大值=10.

【题目】脱贫攻坚,让贫困群众更有幸福感,在党和政府的帮扶下,小刚家的网络商店(简称网店)将顾县豆腐干、莲桥米粉等优质土特产迅速销往全国,小刚家网店中顾县豆腐干和莲桥米粉这两种商品的相关信息如下表:
商品 | 顾县豆腐干 | 莲桥米粉 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 20 | 19 |
售价(元/袋) | 30 | 27 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小刚家网店销售上表中规格的顾县豆腐干和莲桥米粉共1500kg,获得利润1.05万元,求这前五个月小刚家网店销售这种规格的顾县豆腐干和莲桥米粉各多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小刚家网店还能销售上表中规格的顾县豆腐干和莲桥米粉共1000kg,其中,这种规格的顾县豆腐干的销售量不低于300kg.假设这后五个月,销售这种规格的顾县豆腐干x(kg),销售这种规格的顾县豆腐干和莲桥米粉获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小刚家网店销售这种规格的顾县豆腐干和莲桥米粉至少获得总利润多少元.