Question

【题目】如图，扇形OAB的半径OA＝4，圆心角∠AOB＝90°，点C是弧AB上异于A、B的一点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连结DE，过点C作弧AB所在圆的切线CG交OA的延长线于点G．

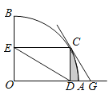
（1）求证：∠CGO＝∠CDE；

（2）若∠CGD＝60°，求图中阴影部分的面积．

Answer 1

【答案】（1）见解析；（2）图中阴影部分的面积为．

【解析】

（1）连接OC交DE于F，根据矩形的判定定理证出四边形CEOD是矩形，根据矩形的性质和等边对等角证出∠FCD＝∠CDF，然后根据切线的性质可得∠OCG＝90°，然后根据同角的余角相等即可证出结论；

（2）根据题意，求出∠COD＝30°，然后利用锐角三角函数求出CD和OD，然后根据扇形的面积公式和三角形的面积公式即可求出结论．

证明：（1）连接OC交DE于F，

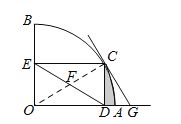
∵CD⊥OA，CE⊥OB，

∴∠CEO＝∠AOB＝∠CDO＝90°，

∴四边形CEOD是矩形，

∴CF＝DF＝EF＝OF，∠ECD＝90°，

∴∠FCD＝∠CDF，∠ECF+∠FCD＝90°，

∵CG是⊙O的切线，

∴∠OCG＝90°，

∴∠OCD+∠GCD＝90°，

∴∠ECF＝∠GCD，

∵∠DCG+∠CGD＝90°，

∴∠FCD＝∠CGD，

∴∠CGO＝∠CDE；

（2）由（1）知，∠CGD＝∠CDE＝60°，

∴∠DCO＝60°，

∴∠COD＝30°，

∵OC＝OA＝4，

∴CD＝2，OD＝2，

∴图中阴影部分的面积＝﹣2×2＝π﹣2．