题目内容
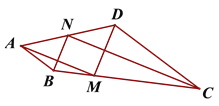
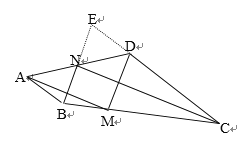
【题目】如图,在四边形ABCD中,∠ABC=150°,∠BCD=30°,点M在BC上,AB=BM,CM=CD,点N为AD的中点,求证:BN⊥CN。
【答案】证明见解析.
【解析】试题分析:延长BN、CD交于点E,根据同旁内角互补,两直线平行,可证AB∥CD,然后根据平行线的性质得到∠BAD=∠ADE,再根据全等三角形的判定“ASA”证得△ABN≌△EDN,得出BN=EN,AB=DE,进而得到CB=CE,最后根据等腰三角形的“三线合一”的性质得证.
试题解析:如图,延长BN、CD交于点E,
∵∠ABC=150°,∠BCD=30°,∴∠ABC+∠BCD=180°,
∴AB∥CD,∴∠BAD=∠ADE,
在△ABN和△EDN中,
∵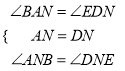
∴△ABN≌△EDN(ASA),
∴BN=EN,AB=DE,又∵AB=BM,∴DE=BM,
∵CM=CD,∴CB=CE,∵BN=EN,∴CN⊥BN.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目