Question

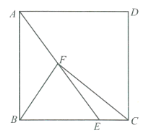
【题目】已知AB⊥DE于A，C，O是AB上一点，且AC＝CO＝OB＝2，以O为圆心作扇形BOF，F到直线AB的距离为．

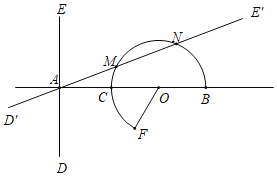
（1）求扇形BOF的面积：

（2）将直线DE绕A点旋转得到直线D'E'；

①当直线D'E'与扇形BOF相切时，求旋转角的大小；

②设直线D'E'与扇形BOF的弧相交于M、N，若AM＝MN，求MN的长．

Answer 1

【答案】（1）；（2）①120°；②

【解析】

（1）根据扇形面积公式即可求扇形BOF的面积：

（2）①根据直线D″E″与扇形BOF相切，即可求旋转角的大小；

②根据垂径定理构造直角三角形根据勾股定理即可求MN的长．

解：如图：

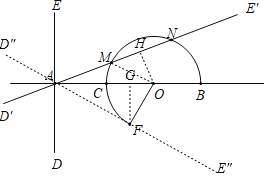
（1）∵AC＝CO＝OB＝2，

以O为圆心作扇形BOF，

∴OB＝OF＝2

过点F作FG⊥BC于点G，

∴FG＝，

∴sin∠GOF＝＝

∴∠GOF＝60°，

∴∠FOB＝120°，

∴S扇形BOF＝＝；

（2）①将直线DE绕A点旋转得到直线D″E″，当直线D″E″与扇形BOF相切时，

设切点为F，

∴OF⊥D″E″，

∴sin∠OAF＝＝

∴∠OAF＝30°

∴∠EAE″＝120°

答：旋转角的大小为120°；

②作OH⊥MN于点H，连接OM，

根据垂径定理，得

MH＝MN，

设MH＝x，则MN＝AM＝2x，

∴AH＝3x，

OM＝OC＝AC＝2，

∴OA＝4，

根据勾股定理，得

OM2﹣MH2＝OA2﹣AH2

即4﹣x2＝16﹣9x2

解得x＝

∴MN＝2x＝．