题目内容
【题目】已知：∠BAC．
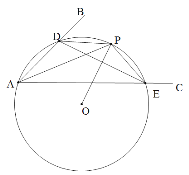
（1）如图，在平面内任取一点O；
（2）以点O为圆心，OA为半径作圆，交射线AB于点D，交射线AC于点E；
（3）连接DE，过点O作线段DE的垂线交⊙O于点P；
（4）连接AP，DP和PE．根据以上作图过程及所作图形，下列四个结论中：
①△ADE是⊙O的内接三角形； ② 
；
③ DE=2PE； ④ AP平分∠BAC．
所有正确结论的序号是______________．
【答案】①④
【解析】
①按照圆的内接三角形的定义判断即可，三顶点都在一个圆周上的三角形，叫做这个圆周的内接三角形；
② 利用垂径定理得到弧长之间的关系即可；
③设OP与DE交于点M，利用垂径定理可得DE⊥OP，DE=2ME，再利用直角三角形中斜边长大于直角边，找到PE与与ME的关系，进一步可以得到DE与PE的关系；
④根据
，即可得到∠DAP=∠PAE，则AP平分∠BAC．
解：①点A、D、E三点均在⊙O上，所以△ADE是⊙O的内接三角形，此项正确；
② ∵DE⊥DE交⊙O于点P
∴
并不能证明
与
、
关系，
∴
不正确；
③设OP与DE交于点M
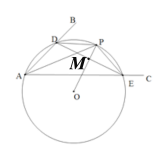
∵DE⊥DE交⊙O于点P
∴DE⊥OP， ME=
DE（垂径定理）
∴△PME是直角三角形
∴ME＜PE
∴
＜PE
∴DE＜2PE
故此项错误.
④∵ （已证）
∴∠DAP=∠PAE（同弧所对的圆周角相等）
∴AP平分∠BAC．
故此项正确.
故正确的序号为：①④
练习册系列答案
相关题目
