题目内容
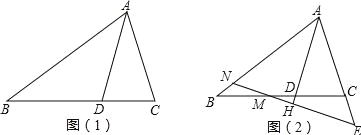
【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC= ![]() °.
°.
(1)如图1,若AB//ON,则①∠ABO的度数是______;②当∠BAD=∠ABD时, ![]() =______;③当∠BAD=∠BDA时,
=______;③当∠BAD=∠BDA时, ![]() =______.
=______.
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
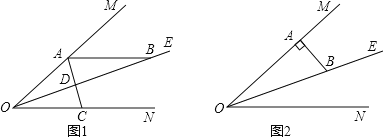
【答案】(1)①20°,②120°,③60°;(2)存在,x=50、20、35或125
【解析】试题分析:(1)①运用平行线的性质以及角平分线的定义,可得①∠ABO的度数;②根据∠ABO、∠BAD的度数以及△AOB的内角和,可得x的值;(2)分两种情况进行讨论:AC在AB左侧,AC在AB右侧,分别根据三角形内角和定理以及直角的度数,可得x的值.
试题解析:如图1,①∵∠MON=36°,OE平分∠MON,
∴∠AOB=∠BON=18,
∵AB∥ON,
∴∠ABO=18;
②当∠BAD=∠ABD时,∠BAD=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°18°×3=126°;
当∠BAD=∠BDA时,∵∠ABO=18°,
∴∠BAD=81°,∠AOB=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°18°18°81°=63°,
故答案为:①18°;②126,63;
(2)如图2,存在这样的x的值,使得△ADB中有两个相等的角。
∵AB⊥OM,∠MON=36,OE平分∠MON,
∴∠AOB=18°,∠ABO=72°,
①当AC在AB左侧时:
若∠BAD=∠ABD=72°,则∠OAC=90°72°=18°;
若∠BAD=∠BDA=180°72°2=54°,则∠OAC=90°54°=36°;
若∠ADB=∠ABD=72°,则∠BAD=36°,故∠OAC=90°36°=54°;
②当AC在AB右侧时:
∵∠ABE=108°,且三角形的内角和为180°,
∴只有∠BAD=∠BDA=180°108°2=36°,则∠OAC=90°+36°=126°.
综上所述,当x=18、36、54、126时,△ADB中有两个相等的角。

【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:
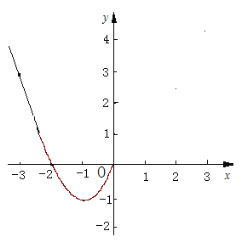
(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________