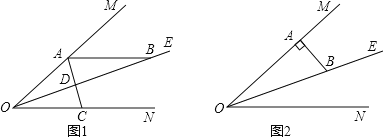题目内容
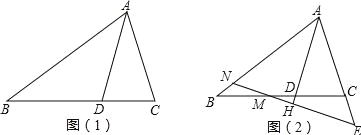
【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
【答案】(1)36 ;72 ;(2)①证明详见解析;②CD=BN+CE,理由详见解析.
【解析】
试题分析:(1)BA=BC,且DB=DA=AC可得∠C=∠ADC=∠BAC=2∠B,∠DAC=∠B,在△ADC中由三角形内角和可求得∠B,∠C;
(2)①由(1)可知∠BAD=∠CAD=36°,且∠AHN=∠AHE=90°,可求得∠ANH=∠AEH=54°,可得AN=AE;
②由①知AN=AE,借助已知利用线段的和差可得CD=BN+CE.
试题解析:(1)∵BA=BC,
∴∠BCA=∠BAC,
∵DA=DB,
∴∠BAD=∠B,
∵AD=AC,
∴∠ADC=∠C=∠BAC=2∠B,
∴∠DAC=∠B,
∵∠DAC+∠ADC+∠C=180°,
∴2∠B+2∠B+∠B=180°,
∴∠B=36°,∠C=2∠B=72°,
故答案为:36;72;
(2)①在△ADB中,∵DB=DA,∠B=36°,
∴∠BAD=36°,
在△ACD中,∵AD=AC,
∴∠ACD=∠ADC=72°,
∴∠CAD=36°,
∴∠BAD=∠CAD=36°,
∵MH⊥AD,
∴∠AHN=∠AHE=90°,
∴∠AEN=∠ANE=54°,
∴AN=AE,
即△ANE是等腰三角形;
②CD=BN+CE.
证明:由①知AN=AE,
又∵BA=BC,DB=AC,
∴BN=AB﹣AN=BC﹣AE,CE=AE﹣AC=AE﹣BD,
∴BN+CE=BC﹣BD=CD,
即CD=BN+CE.