题目内容
【题目】如图,AB为⊙O直径,C为⊙O上一点,点D是 ![]() 的中点,DE⊥AC于E,DF⊥AB于F.
的中点,DE⊥AC于E,DF⊥AB于F. 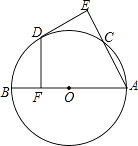
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若OF=4,求AC的长度.
【答案】
(1)解:DE与⊙O相切.
证明:连接OD、AD,

∵点D是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠DAO=∠DAC,
∵OA=OD,
∴∠DAO=∠ODA,
∴∠DAC=∠ODA,
∴OD∥AE,
∵DE⊥AC,
∴DE⊥OD,
∴DE与⊙O相切
(2)解:连接BC交OD于H,延长DF交⊙O于G,

由垂径定理可得:OH⊥BC, ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DG=BC,
∴弦心距OH=OF=4,
∵AB是直径,
∴BC⊥AC,
∴OH∥AC,
∴OH是△ABC的中位线,
∴AC=2OH=8.
【解析】(1)先连接OD、AD,根据点D是 ![]() 的中点,得出∠DAO=∠DAC,进而根据内错角相等,判定OD∥AE,最后根据DE⊥OD,得出DE与⊙O相切;(2)先连接BC交OD于H,延长DF交⊙O于G,根据垂径定理推导可得OH=OF=4,再根据AB是直径,推出OH是△ABC的中位线,进而得到AC的长是OH长的2倍.
的中点,得出∠DAO=∠DAC,进而根据内错角相等,判定OD∥AE,最后根据DE⊥OD,得出DE与⊙O相切;(2)先连接BC交OD于H,延长DF交⊙O于G,根据垂径定理推导可得OH=OF=4,再根据AB是直径,推出OH是△ABC的中位线,进而得到AC的长是OH长的2倍.
【考点精析】根据题目的已知条件,利用三角形中位线定理和垂径定理的相关知识可以得到问题的答案,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目