��Ŀ����
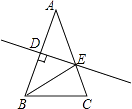
����Ŀ����ͼ��������ABCD�Խ��߽���Ϊ����ԭ�㣬����ƽ��ֱ������ϵ��A��B���������ֱ�Ϊ����2 ![]() ��0������0����
��0������0���� ![]() ����ֱ��DE��DC��AC��E������P�ӵ�A��������ÿ��2����λ���ٶ�����A��D��C��·�����յ�C�����˶������PDE�����ΪS��S��0������P���˶�ʱ��Ϊt�룮
����ֱ��DE��DC��AC��E������P�ӵ�A��������ÿ��2����λ���ٶ�����A��D��C��·�����յ�C�����˶������PDE�����ΪS��S��0������P���˶�ʱ��Ϊt�룮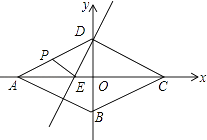
��1����ֱ��DE�Ľ���ʽ��
��2����S��t֮��ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3����tΪ��ֵʱ����EPD+��DCB=90�㣿�������ʱֱ��BP��ֱ��AC������ǵ�����ֵ��
���𰸡�
��1��
�⣺�����εĶԳ��Կɵã�C��2 ![]() ��0����D��0��
��0����D��0�� ![]() ����
����
��OD= ![]() ��OC=2
��OC=2 ![]() ��tan��DCO=
��tan��DCO= ![]() =
= ![]() ��
��
��DE��DC��
���EDO+��CDO=90�㣬
�ߡ�DCO+��CD��=90�㣬
���EDO=��DCO��
��tan��EDO=tan��DCO= ![]() ��
��
�� ![]() ��
��
��OE= ![]() ��
��
��E���� ![]() ��0����
��0����
��D��0�� ![]() ����
����
��ֱ��DE����ʽΪy=2x+ ![]()
��2��
�⣺�ɣ�1����E���� ![]() ��0����
��0����
��AE=AO��OE=2 ![]() ��
�� ![]() =
= ![]() ��
��
���ݹ��ɶ����ã�DE= ![]() =
= ![]() ��
��
�����εı߳�Ϊ5��
��ͼ1��
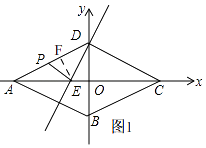
����E��EF��AD��
��sin��DAO= ![]() ��
��
��EF= ![]() =
= ![]() ��
��
����P��AD�����˶�����0��t�� ![]() ��
��
S= ![]() PD��EF=
PD��EF= ![]() ����5��2t����
����5��2t���� ![]() =��
=�� ![]() t+
t+ ![]() ��
��
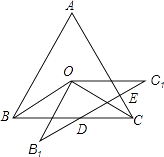
��ͼ2��
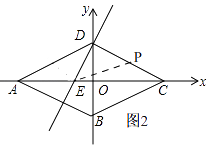
��P��DC�����˶�ʱ���� ![]() ��t��5ʱ��
��t��5ʱ��
S= ![]() PD��DE=
PD��DE= ![]() ����2t��5����
����2t��5���� ![]() =
= ![]() t��
t�� ![]() ��
��
��S= 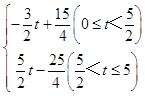
��3��
�⣺��BP��AC�ཻ�ڵ�Q��
������ABCD����DAB=��DCB��DE��DC��
��DE��AB��
���DAB+��ADE=90�㣬
���DCB+��ADE=90�㣬
��Ҫʹ��EPD+��DCB=90�㣬
���EPD=��ADE��
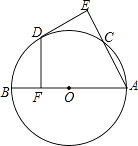
����P��AD���˶�ʱ����ͼ3��
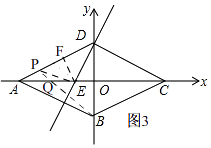
�ߡ�EPD=��ADE��
��EF��ֱƽ����PD��
��AP=AD��2DF=AD��2 ![]() ��
��
��2t=5�� ![]() ��
��
��t= ![]() ��
��
��ʱAP=1��
��AP��BC��
���APQ�ס�CBQ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
��AQ= ![]() ��
��
��OQ=OA��AQ= ![]() ��
��
��Rt��OBQ��tan��OQB= ![]() =
= ![]() =
= ![]() ��
��
����P��DC���˶�ʱ����ͼ4��
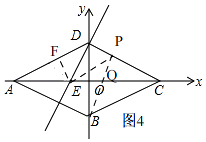
�ߡ�EPD=��ADE����EDP=��EFD=90��
���EDP�ס�EFD��
�� ![]() ��
��
��DP= ![]() =
= 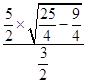 =
= ![]() ��
��
��2t=AD��DP=5+ ![]() ��
��
��t= ![]() ��
��
��ʱCP=DC��DP=5�� ![]() =
= ![]() ��
��
��PC��AB��
���CPQ�ס�ABQ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
��CQ= ![]() ��
��
��OQ=OC��CQ=2 ![]() ��
�� ![]() =
= ![]() ��
��
��Rt��OBD��tan��OQB= ![]() =
= ![]() =1��
=1��
������t= ![]() ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ
ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ ![]() ��
��
��t= ![]() ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ1
ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ1
����������1���������εĶԳ��Եó���C��D���꣬Ȼ���á�DCO������ֵ���Լ��Ƚǵ����Ǻ���ֵ����г����̣�����ô���ϵ�������ֱ��DE����ʽ����2����������εı߳��������EF���ֵ�P��AD��DC���ϣ��������ʽ��⣻��3���������EPD=��ADE������������������εı߳������������ʱ��t�������������εı���ʽ�����������OQ����ֱ�������μ��ɣ�

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д�