ƒøƒ⁄»ð
°æƒø°ø£®1£©π€≤ÏÕº–Œ£∫
»ÁÕº1£¨°˜ABC÷–£¨AB=AC£¨°œBAC=45°„£¨CD°ÕAB£¨AE°ÕBC£¨¥π◊„∑÷±Œ™D°¢E£¨CD”ÎAEΩª”⁄µ„F£Æ
¢Ÿ–¥≥ˆÕº1÷–À˘”–µƒ»´µ»»˝Ω«–Œ_________________£ª
¢⁄œþ∂ŒAF”Îœþ∂ŒCEµƒ ˝¡øπÿœµ «_________________£ª
£®2£©Œ ÂÃΩæø£∫
»ÁÕº2£¨°˜ABC÷–£¨°œBAC=45°„£¨AB=BC£¨AD∆Ω∑÷°œBAC£¨AD°ÕCD£¨¥π◊„Œ™D£¨AD”ÎBCΩª”⁄µ„E£Æ
«Û÷§£∫AE=2CD£Æ
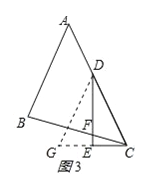
£®3£©Õÿ’π—”…Ï£∫
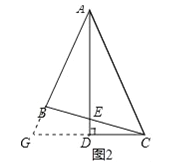
»ÁÕº3£¨°˜ABC÷–£¨°œBAC=45°„£¨AB=BC£¨µ„D‘⁄AC…œ£¨°œEDC=![]() °œBAC£¨DE°ÕCE£¨¥π◊„Œ™E£¨DE”ÎBCΩª”⁄µ„F£Æ
°œBAC£¨DE°ÕCE£¨¥π◊„Œ™E£¨DE”ÎBCΩª”⁄µ„F£Æ
«Û÷§£∫DF=2CE£Æ

°æ¥∞∏°ø£®1£©¢Ÿ°˜ABE°’°˜ACE£¨°˜ADF°’°˜CDB£ª¢⁄AF=2CE£ª£®2£©¥∞∏º˚Ω‚Œˆ£ª£®3£©¥∞∏º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
‘Â![]() π€≤ÏÕº–Œ£∫¢Ÿ”…»´µ»»˝Ω«–Œµƒ≈–∂®∑Ω∑®»ð“◊µ√≥ˆΩ·π˚£ª
π€≤ÏÕº–Œ£∫¢Ÿ”…»´µ»»˝Ω«–Œµƒ≈–∂®∑Ω∑®»ð“◊µ√≥ˆΩ·π˚£ª
¢⁄”…»´µ»»˝Ω«–Œµƒ–‘÷ º¥ø…µ√≥ˆΩ·¬€£ª![]() Œ ÂÃΩæø£∫—”≥§
Œ ÂÃΩæø£∫—”≥§![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨”…ASA÷§√˜
£¨”…ASA÷§√˜![]() °’
°’![]() £¨µ√≥ˆ∂‘”¶±þœýµ»
£¨µ√≥ˆ∂‘”¶±þœýµ»![]() º¥
º¥![]() ÷§≥ˆ
÷§≥ˆ![]() ”…ASA÷§√˜
”…ASA÷§√˜![]() °’
°’![]() µ√≥ˆ
µ√≥ˆ![]() º¥ø…£Æ
º¥ø…£Æ![]() Õÿ’π—”…Ï£∫◊˜DG°ÕBC”⁄µ„H£¨ΩªCEµƒ—”≥§œþ”⁄G£¨Õ¨…œ÷§√˜»˝Ω«–Œ»´µ»£¨µ√≥ˆ
Õÿ’π—”…Ï£∫◊˜DG°ÕBC”⁄µ„H£¨ΩªCEµƒ—”≥§œþ”⁄G£¨Õ¨…œ÷§√˜»˝Ω«–Œ»´µ»£¨µ√≥ˆ![]() º¥ø…£Æ
º¥ø…£Æ
‘Ã‚Ω‚Œˆ£∫
£®1£©π€≤ÏÕº–Œ£∫
¢Ÿ°˜ABE°’°˜ACE£¨°˜ADF°’°˜CDB£ª
¢⁄AF=2CE£ª
£®2£©Œ ÂÃΩæø£∫
÷§√˜£∫—”≥§AB°¢CDΩª”⁄µ„G£¨»ÁÕº2À˘ æ£∫
°þAD∆Ω∑÷°œBAC£¨
°ý°œCAD=°œGAD£¨
°þAD°ÕCD£¨
°ý°œADC=°œADG=90°„£¨
‘⁄°˜ADC∫Õ°˜ADG÷–£¨
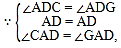 £¨
£¨
°ý°˜ADC°’°˜ADG£®ASA£©£¨
°ýCD=GD£¨
º¥CG=2CD£¨
°þ°œBAC=45°„£¨AB=BC£¨
°ý°œABC=90°„£¨
°ý°œCBG=90°„£¨
°ý°œG+°œBCG=90°„£¨
°þ°œG+°œBAE=90°„£¨
°ý°œBAE=°œBCG£¨
‘⁄°˜ABE∫Õ°˜CBG÷–£¨
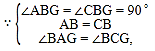
°ý°˜ADC°’°˜CBG£®ASA£©£¨
°ýAE=CG=2CD£Æ
£®3£©Õÿ’π—”…Ï£∫
÷§√˜£∫◊˜DG°ÕBC”⁄µ„H£¨ΩªCEµƒ—”≥§œþ”⁄G£¨
°þ°œBAC=45°„£¨AB=BC£¨
°ýAB°ÕBC£¨
°ýDG°ŒAB£¨
°ý°œGDC=°œBAC=45°„£¨
°ý°œEDC=![]() °œBAC=22.5°„=°œEDG£¨DH=CH£¨
°œBAC=22.5°„=°œEDG£¨DH=CH£¨
”÷°þDE°ÕCE£¨
°ý°œDEC=°œDEG=90°„£¨
‘⁄°˜DEC∫Õ°˜DEG÷–£¨
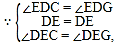
°ý°˜DEC°’°˜DEG£®ASA£©£¨
°ýDC=DG£¨CG=2CE£¨
°þ°œDHF=°œCEF=90°„£¨°œDFH=°œCFE£¨
°ý°œFDH=°œGCH£¨
‘⁄°˜DHF∫Õ°˜CHG÷–£¨
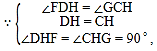
°ý°˜DHF°’°˜CHG£®ASA£©,
°ýDF=CG=2CE£Æ