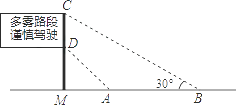题目内容
【题目】如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)
【答案】解:过点C作CM⊥AB交AB延长线于点M,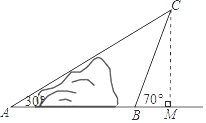
由题意得:AC=40×10=400(米).
在直角△ACM中,∵∠A=30°,
∴CM= ![]() AC=200米,AM=
AC=200米,AM= ![]() AC=200
AC=200 ![]() 米.
米.
在直角△BCM中,∵tan20°= ![]() ,
,
∴BM=200tan20°,
∴AB=AM﹣BM=200 ![]() ﹣200tan20°=200(
﹣200tan20°=200( ![]() ﹣tan20°),
﹣tan20°),
因此A,B两地的距离AB长为200( ![]() ﹣tan20°)米.
﹣tan20°)米.
【解析】根据在直角三角形中,30度角所对的边是斜边的一半和勾股定理,求出CM=AC÷2、AM的值,再由解直角三角形中正切的定义,求出BM=200tan20°,得到AB=AM﹣BM的值.
【考点精析】通过灵活运用关于方向角问题,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角即可以解答此题.

练习册系列答案
相关题目