题目内容
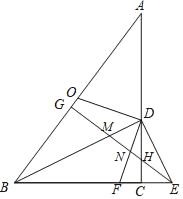
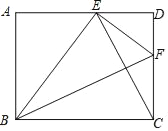
【题目】如图,在矩形ABCD中,点E是边AD上的点,EF⊥BE,交边CD于点F,联结CE、BF,如果tan∠ABE=![]() ,那么CE:BF=_____.
,那么CE:BF=_____.
【答案】4:5
【解析】
首先证明B,C,F,E四点共圆,推出∠EBF=∠ECF,推出△BEF∽△CDE,可得![]() =
=![]() ,再证明∠DEF=∠ABE,推出tan∠ABE=tan∠DEF=
,再证明∠DEF=∠ABE,推出tan∠ABE=tan∠DEF=![]() =
=![]() ,设DF=3k,DE=4k,可得EF=5k,由此即可解决问题.
,设DF=3k,DE=4k,可得EF=5k,由此即可解决问题.
解:∵四边形ABCD是矩形,
∴∠A=∠D=∠BCD=90°,
∵EF⊥BE,
∴∠BEF=90°,
∴∠BEF+∠BCF=180°,
∴B,C,F,E四点共圆,
∴∠EBF=∠ECF,∵∠BEF=∠D=90°,
∴△BEF∽△CDE,
∴![]() =
=![]() ,
,
∵∠ABE+∠AEB=90°,∠AEB+∠DEF=90°,
∴∠DEF=∠ABE,
∴tan∠ABE=tan∠DEF=![]() =
=![]() ,
,
设DF=3k,DE=4k,
∴EF=5k,
∴![]() =
=![]() =
=![]() ,
,
故答案为:4:5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目