ЬтФПФкШн
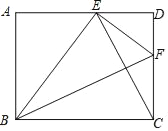
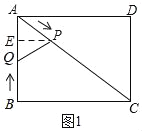
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН6ЃЌBCЃН8ЃЎЖЏЕуPДгЕуAГіЗЂбиACЯђжеЕуCдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуBГіЗЂбиBAЯђЕуAдЫЖЏЃЌЕНДяAЕуЪБЭЃжЙдЫЖЏЃЎЕуPвВЭЌЪБЭЃжЙЃЎЕуPЃЌQдЫЖЏЫйЖШОљЮЊУПУы1ИіЕЅЮЛГЄЖШЃЌСЌНгPQЃЌЩшдЫЖЏЪБМфЮЊt(tЃО0)УыЃЎ
(1)ЕБЕуQДгBЕуЯђAЕудЫЖЏЪБ(ЮДЕНДяAЕу)ЃЌ
ЂйЕБtЃН_____ЪБPQЁЮBC
ЂкЧѓЁїAPQЕФУцЛ§SЙигкtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіtЕФШЁжЕЗЖЮЇЃЛ
(2)АщЫцзХPЃЌQСНЕуЕФдЫЖЏЃЌЯпЖЮPQЕФДЙжБЦНЗжЯпЮЊlЃК
ЂйЕБlОЙ§ЕуAЪБЃЌЩфЯпQPНЛADгкЕуEЃЌЧѓДЫЪБЕФtЕФжЕКЭAEЕФГЄЃЛ
ЂкЕБlОЙ§ЕуBЪБЃЌЧѓtЕФжЕЃЎ

ЁОД№АИЁП(1)Ђй![]() УыЃЛЂкSЁїAPQЃНЉ
УыЃЛЂкSЁїAPQЃНЉ![]() +
+![]() t(0ЃМtЁм6)ЃЛ(2)ЂйtЃН3ЃЌAEЃН6ЃЛЂкtЃН5ЃЎ
t(0ЃМtЁм6)ЃЛ(2)ЂйtЃН3ЃЌAEЃН6ЃЛЂкtЃН5ЃЎ
ЁОНтЮіЁП
(1)ЂйвђЮЊPQЁЮBCЃЌРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЃЌПЩЕУ![]() ЃЌевЕНЙигкtЕФЗНГЬЃЌЧѓНтМДПЩЃЛЂкЙ§PзїPEЁЭABгкEЃЌРћгУЁЯBACЕФе§ЯвЃЌПЩвдЧѓГіPEЕФГЄЃЌзюКѓевЕНSгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЌевЕНЙигкtЕФЗНГЬЃЌЧѓНтМДПЩЃЛЂкЙ§PзїPEЁЭABгкEЃЌРћгУЁЯBACЕФе§ЯвЃЌПЩвдЧѓГіPEЕФГЄЃЌзюКѓевЕНSгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЂйвђЮЊlЮЊPQЕФДЙжБЦНЗжЯпЧвЙ§ЕуAЃЌЫљвдAP=AQЃЌгЩДЫПЩвдЧѓГіtЕФжЕЃЌбгГЄQPНЛCDгкMЃЌШнвзЕУЕНЁїAPQКЭЁїCPMЯрЫЦЃЌевЕНЯрЫЦБШПЩЧѓГіAEЕФГЄЃЛЂкЕБlОЙ§BЪБЃЌПЩЕУBQ=BP=APЃЌЙ§PзїPGЁЭABгкGЃЌРћгУШ§ЯпКЯвЛПЩЕУAG=BGЃЌРћгУPGЁЮBCЃЌПЩзЊЛЏГіPвВЮЊACЕФжаЕуЃЌНјЖјПЩЧѓГіAPЕФжЕЃЌзюКѓПЩевЕНtЕФжЕ.
НтЃК(1)ЂйгЩЬтвтЕУЃКBQЃНAPЃНtЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯABCЃН90ЁуЃЌ
ЁпABЃН6ЃЌBCЃН8ЃЌ
ЁрACЃН10ЃЌAQЃН6ЉtЃЌ
ЁпPQЁЮBCЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
tЃН![]() ЃЌ
ЃЌ
дђЕБtЃН![]() УыЪБЃЌPQЁЮBCЃЌ
УыЪБЃЌPQЁЮBCЃЌ
ЙЪД№АИЮЊЃК![]() УыЃЛ
УыЃЛ
ЂкШчЭМ1ЃЌЙ§PзїPEЁЭABгкEЃЌ
sinЁЯBACЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌPEЃН
ЃЌPEЃН![]() tЃЌ
tЃЌ
ЁрSЁїAPQЃН![]() AQPEЃН
AQPEЃН![]() (6Љt)
(6Љt)![]()
![]() tЃНЉ
tЃНЉ![]() +
+![]() t(0ЃМtЁм6)ЃЛ
t(0ЃМtЁм6)ЃЛ
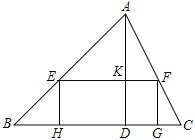
(2)ЂйШчЭМ2ЃЌбгГЄCDНЛQPгкMЃЌ
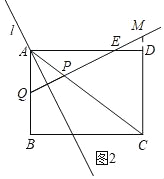
ЁпЯпЖЮPQЕФДЙжБЦНЗжЯпЮЊlОЙ§ЕуAЃЌ
ЁрAQЃНAPЃЌМД6ЉtЃНtЃЌ
ЁрtЃН3ЃЌ
ЁрAQЃНAPЃН3ЃЌCPЃН10Љ3ЃН7ЃЌ
ЁпAQЁЮCDЃЌ
ЁрЁїAQPЁзЁїCMPЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌCMЃН7ЃЌ
ЃЌCMЃН7ЃЌ
ЁрDMЃН7Љ6ЃН1ЃЌ
ЁпAQЁЮDMЃЌ
ЁрЁїAQEЁзЁїDMEЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпAE+DEЃН8ЃЌ
ЁрAEЃН6ЃЛ
ЂкШчЭМ3ЃЌСЌНгPBЃЌЙ§PзїPGЁЭABгкGЃЌдђPGЁЮBCЃЌ
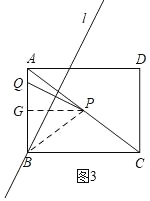
ЁпЯпЖЮPQЕФДЙжБЦНЗжЯпlОЙ§ЕуBЃЌ
ЁрPBЃНBQЃНtЃНAPЃЌ
ЁрAGЃНBGЃЌ
ЁрAPЃНPCЃН![]() ACЃН5ЃЌ
ACЃН5ЃЌ
ЁрtЃН5ЃЎ

ЁОЬтФПЁПФГЭЌбЇдкРћгУУшЕуЗЈЛЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЃН0ЃЉЕФЭМЯѓЪБЃЌЯШШЁздБфСПxЕФвЛаЉжЕЃЌМЦЫуГіЯргІЕФКЏЪ§жЕyЃЌШчЯТБэЫљЪОЃК
x | Ё | 0 | 1 | 2 | 3 | 4 | Ё |
y | Ё | Љ3 | 0 | Љ1 | 0 | Љ3 | Ё |
НгзХЃЌЫћдкУшЕуЪБЗЂЯжЃЌБэИёжагавЛзщЪ§ОнМЦЫуДэЮѓЃЌЫћМЦЫуДэЮѓЕФвЛзщЪ§ОнЪЧЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()