Question

【题目】阅读理解：

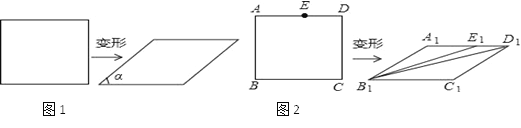
我们知道，四边形具有不稳定性，容易变形，如图1，一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把的值叫做这个平行四边形的变形度．

（1）若矩形发生变形后的平行四边形有一个内角是120度，则这个平行四边形的变形是　 ．

猜想证明：

（2）设矩形的面积为S1，其变形后的平行四边形面积为S2，试猜想S1，S2， 之间的数量关系，并说明理由；

拓展探究：

（3）如图2，在矩形ABCD中，E是AD边上的一点，且AB2=AEAD，这个矩形发生变形后为平行四边形A1B1C1D1，E1为E的对应点，连接B1E1，B1D1，若矩形ABCD的面积为4 （m＞0），平行四边形A1B1C1D1的面积为2（m＞0），试求∠A1E1B1+∠A1D1B1的度数．

Answer 1

【答案】（1）；（2），理由见解析；（3）∠A1E1B1+∠A1D1B1=30°．

【解析】解：（1）；

（2）=，

理由：如图1，

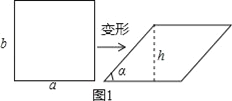
设矩形的长和宽分别为a，b，变形后的平行四边形的高为h，

∴S1=ab，S2=ah，∴==，

∵sinα= ∴=，∴=；

（3）∵AB2=AEAD，

∴A1B12=A1E1A1D1，即=，

∵∠B1A1E1=∠D1A1B1，∴△B1A1E1∽△D1A1B1，

∴∠A1B1E1=∠A1D1B1，

∵A1D1∥B1C1，

∴∠A1E1B1=∠C1B1E1，

∴∠A1E1B1+∠A1D1B1=∠C1E1B1+∠A1B1E1=∠A1B1C1，

由（2）知=可知/span>==2，

∴sin∠A1B1C1=，

∴∠A1B1C1=30°，

∴∠A1E1B1+∠A1D1B1=30°．