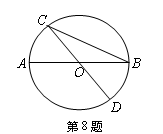
题目内容
如图 ,
, 于
于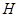 ,
,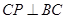 交
交 于点
于点 ,
, ,则
,则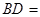 ___________________
___________________
 ,
, 于
于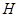 ,
,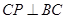 交
交 于点
于点 ,
, ,则
,则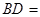 ___________________
___________________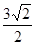
∵BD与AH交于点P,则由AC=AD,AH⊥CD得∠ACH=∠ADH.
又AB=AD,故∠ADB=∠ABD.
从而,∠ABP=∠ACP.可知A、B、C、P四点共圆.
∵∠APC=90°+∠PCH=∠BCD,∠CBP=∠CAP,
∴△APC∽△BCD.
∴AC•BC=AP•BD.
∴BD=AC•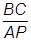 ,
,
∴BD=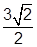
又AB=AD,故∠ADB=∠ABD.
从而,∠ABP=∠ACP.可知A、B、C、P四点共圆.
∵∠APC=90°+∠PCH=∠BCD,∠CBP=∠CAP,
∴△APC∽△BCD.
∴AC•BC=AP•BD.
∴BD=AC•
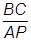 ,
,∴BD=
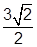

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
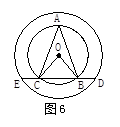
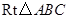 中,
中,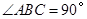 ,以
,以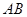 为直径的
为直径的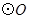 交
交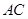 于点
于点 ,过点
,过点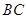 于
于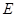
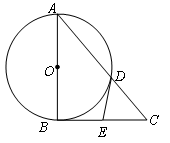

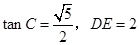 ,求
,求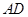 的长.
的长.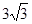 ,则圆锥的侧面积是 ▲ .
,则圆锥的侧面积是 ▲ .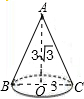
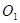 与⊙
与⊙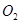 的半径分别为5和2,
的半径分别为5和2,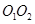 =3,则⊙
=3,则⊙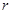 为3cm,⊙O2的半径R为4cm,两圆的圆心距O1O2为1cm,则这两圆的位置关系是
为3cm,⊙O2的半径R为4cm,两圆的圆心距O1O2为1cm,则这两圆的位置关系是