Question

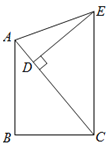
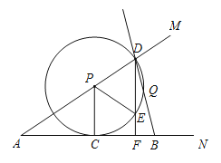
【题目】已知点P为∠MAN边AM上一动点，⊙P切AN于点C，与AM交于点D（点D在点P的右侧），作DF⊥AN于F，交⊙O于点E．

（1）连接PE，求证：PC平分∠APE；

（2）若DE＝2EF，求∠A的度数；

（3）点B为射线AN上一点，且AB＝8，射线BD交⊙P于点Q，sin∠A＝．在P点运动过程中，是否存在某个位置，使得△DQE为等腰三角形？若存在，求出此时AP的长；若不存在，请说明理由．

Answer 1

【答案】（1）证明见解析；（2）∠PAC＝30°；（3）存在，AP的长为6或或．

【解析】

（1）根据已知条件以及切线的性质可得PC//DF，再利用平行线的性质和等腰三角形的性质可以证得∠APC＝∠EPC，即可得证结论；

（2）添加辅助线PH⊥DE于H，根据已知条件可得DH＝HE＝EF＝HF＝PC＝PD，进一步可判定∠DPH＝30°，最后利用平行线的性质即可推导出∠A的度数；

（3）分①DQ＝QE②DE＝QE③DQ＝DE三种情况进行讨论即可．

解：（1）证明：∵AN切⊙O于点C

∴PC⊥AN

∵DF⊥AN

∴PC//DF

∴∠APC＝∠PDE， ∠EPC＝∠PED

∵PD＝PE

∴∠PED＝∠PDE

∴∠APC＝∠EPC，即PC平分∠APE

（2）作PH⊥DE于H，如图：

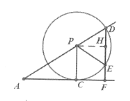
∵PD＝PE，DE＝2EF

∴DH＝HE＝EF＝HF＝PC＝PD

∴∠DPH＝30°

∵PH//AF

∴∠PAC＝∠DPH＝30°

（3）①当DQ＝QE时，如图1

连接PQ，可证得PQ//AB

∴∠PDQ＝∠DQP＝∠DBA

∴AD＝AB＝8

∵设PC＝r，AP＝3r

∴AD＝4r

∴4r＝8

∴r＝2

∴AP＝3r＝6

②当DE＝QE时， 记⊙P与AD的另一交点为K，连接KE，如图：

则∠QDE＝∠EQD＝∠DKE＝∠DAF

在Rt△ADF中，DF＝AD＝r

AF＝DF＝r

在Rt△DBF中，BF＝DF＝r

AB＝AF－BF＝r＝8

r＝，AP＝3r＝

③当DQ＝DE时，连接QK连接QE交AD于I，作QG⊥KE于点G，如图：

则∠GQE＝∠IKE＝∠A

在Rt△QGE中，设GE＝2x，则QE＝3GE＝6x，IE＝3x

QG＝GE＝x

则KG＝KE－EG＝7x

tan∠QKG＝＝，

∵∠BDF＝∠QKE

∴ tan∠BDF＝ tan∠QKE，BF＝DF＝

AB＝AF＋BF＝＝8，

r＝，AP＝3r＝

故答案是：（1）证明见解析；（2）∠PAC＝30°；（3）存在，AP的长为6或或