题目内容
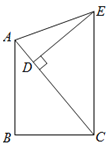
【题目】如图，△ABC为直角三角形，∠B＝90°，AC边上取一点D，使CD＝AB．分别过点C作CE⊥BC，过点D作DE⊥AC，CE，DE相交于E，连结AE．
（1）求证：△ABC≌△CDE；
（2）若∠AED＝20°，求∠ACE的度数．
【答案】（1）证明见解析；（2）∠ACE＝40°．
【解析】
（1）由垂直定义以及平行线的性质得出
、
，再利用角边角定理即可判定
；
（2）根据已知条件先求得
，再由（1）的结论可推出
，从而得到
，进一步利用角的和差以及直角三角形两锐角互余即可得解．
（1）证明：∵∠B＝90°，CE⊥BC
∴AB∥CE
∴∠BAC＝∠ECD
∵DE⊥AC
∴∠EDC＝∠B＝90°
∵CD＝AB
∴
（2）∵DE⊥AC
∴∠ADE＝90°
∵∠AED＝20°
∴∠EAD＝70°
∵△ABC≌△CDE
∴AC＝CE
∴∠AEC＝∠CAE＝70°
∴∠ACE＝40°
故答案是：（1）见解析（2）
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
