Question

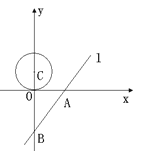
【题目】△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).

(1)如图①,当点C与点O重合时,求直线BD的表达式;

(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;

(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2)时,求∠ODB的正切值.

Answer 1

【答案】（1）y=x-.（2）点B的坐标为(8,-4).（3）.

【解析】试题分析：（1）先根据等边三角形的性质求出B点的坐标，直接运用待定系数法就可以求出直线BD的解析式。

（2）作BE⊥x轴于E，就可以得出∠AEB=90°，由圆的切线的性质就可以而出B的纵坐标，由直角三角形的性质就可以求出B点的横坐标，从而得出结论。

（3）以点B为圆心，AB为半径作⊙B，交y轴于点C、E，过点B作BF⊥CE于F，连接AE．根据等边三角形的性质、圆心角与圆周角之间的关系及勾股定理就可以点B的坐标，作BQ⊥x轴于点Q，根据正切值的意义就可以求出结论。