题目内容
【题目】已知直线l与直线l外一点P,求作:过点P且垂直于直线l的垂线a(尺规作图).
现给出一种作法,如下:
步骤一:在直线l外取一点E,以点P为圆心,以线段PE为半径画弧,交直线l于点M,N;
步骤二:分别以点M、N为圆心,大于![]() 线段MN为半径画弧,过两弧的交点的直线a就是所求作的垂线.
线段MN为半径画弧,过两弧的交点的直线a就是所求作的垂线.
(1)按上述操作步骤,请成功作出过点P且垂直于直线l的垂线a.(符合要求的一种图形),并说明理由.
(2)从你作图的过程中,思考要保证这种作法顺利作出,线段PE应该满足什么条件?
(3)为了避免这种情况产生,小明说只要在直线l上取点E好了,并给出了画法,画法对吗?请说明理由.
(作法:在直线l上取两点B、D,以P为圆心,以PD 为半径画圆交直线l于点E,以P为圆心,以PB 为半径画圆交直线l于点F,其中较小圆分别交PB,PF于点M、N,连接E、N和D、M,EN和MD相交于点H,则PH就是所求的垂线.)
(4)请在直线l上取点E,用直尺和圆规过点P且垂直于直线l的垂线a(与小明不同的方法,并要求尽可能简单).
【答案】答案见解析.
【解析】试题分析:(1)、分点E、点P在直线l的异侧、同侧两种情况来分别进行讨论,从而根据圆的性质得出答案;(2)、根据第一题的情况分析得出线段PE要大于点P到直线的距离;(3)、连接MN,根据题意得出△PMH和△PNH全等,然后根据圆心角的逆定理得出垂线;(4)、利用直径所对的圆周角是直角.
试题解析:(1)、根据点E、点P与直线l的位置关系可分为两种情况:
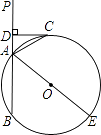
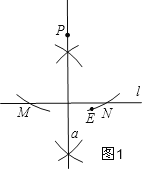
i)点E、点P在直线l的异侧,如图1所示,
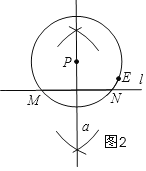
ii)点E、点P在直线l的同侧,再根据点P到直线l 的距离与半径PE长度的比较,圆P与直线l的位置关系可分为三种情况:①圆P与直线l相交,且有两个交点,如图2;
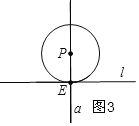
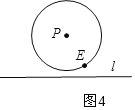
②、圆P与直线l相交,且有一个交点,如图3;③圆P与直线l相离,如图4.
理由如下:
图1,解法:根据第二步作法可得直线a是线段MN的中垂线a, ∵半径PM=PN;
∴点P在线段MN的中垂线; ∴点P在直线a上;
图2,解法:同第一题解法一样;
图3,圆P与直线l交点M,N重合,不符合要求,因此不予讨论;
图4中的圆P不能与直线l相交于点M、N两点,因此不能做出直线a.
(2)、根据第一题的情况分析得出线段PE要大于点P到直线的距离.
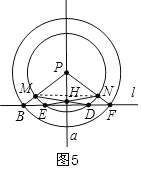
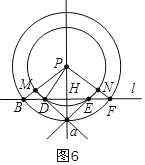
(3)、正确.根据点E和点D在直线PH的同侧(如图6)或异侧(如图5)两种画法如下:
图5理由: 连接MN,可得MN∥BF, ∴∠MNE=∠NED, ∴![]() =
=![]() , ∴∠NMD=∠MNE,
, ∴∠NMD=∠MNE,
∴MH=NH, 由△PMH≌△PNH, ∴∠MPH=∠NPH, ∴PH平分弧MN,即PH垂直ED,
所以PH就是所求的垂线;
图⑥理由:同图⑤证明.
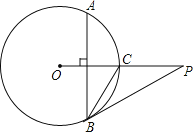
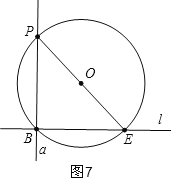
(4)、第一种方法,如图7:
原理:利用直径所对的圆周角是直角,即直径PE所对的∠PBE是直角.
作法:在直线l上取一点E,连接PE,取线段PE中点O,以点O为圆心,线段PO为半径作圆,交直线于点B,作直线PB就是所求的直线a;
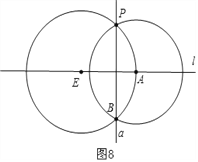
第二种方法,如图8:原理:由半径PE=BE可得点E在线段PB的中垂线上,同理可得点A在线段BP的中垂线上,所以直线l是线段BP的中垂线,即直线BP就是所求的直线a;
作法:在直线l上取点E和点A,然后以点E为圆心,线段PE为半径作圆,再以点A为圆心,线段PA为半径作圆,两圆相交于点P和点B.直线BP就是所求的直线a.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
长方体 | 8 | 12 | |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是E=________;
(3)一个多面体的面数比顶点数大8,棱数为30,则这个多面体的面数是多少?