题目内容
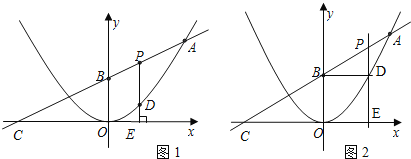
【题目】如图已知二次函数y=ax2图象的顶点为原点，直线y=
x+4的图象与该二次函数的图象交于A点（8，8），直线与x轴的交点为C，与y轴的交点为B．
（1）求这个二次函数的解析式与B点坐标；
（2）P为线段AB上的一个动点（点P与A，B不重合），过P作x轴的垂线与这个二次函数的图象交于D点，与x轴交于点E．设线段PD的长为h，点P的横坐标为t，求h与t之间的函数关系式，并写出自变量t的取值范围（图1）；
（3）在（2）的条件下，连接BD，当动点P在线段AB上移动时，点D也在抛物线上移动，线段BD也绕点B转动，当BD∥x轴时（图2），请求出P点的坐标．
【答案】（1）这个二次函数的解析式y=
x2．B点的坐标为（0，4）．（2）h=﹣
t2+
t+4（0＜t＜8）．（3）P点坐标为（4
，4+2）．
【解析】
试题分析：（1）由二次函数的图象过点A（8，8），将其代入函数解析式中即可求得a值，将x=0代入直线方程，即可求得B点坐标；
（2）由P、D横坐标都为t，将其分别代入二次函数和直线解析式，用t表现出P、D点纵坐标，二者相减即可找到h与t的关系，因为P在线段BA上，由此可找出t的范围；
（3）BD平行x轴，可知，B、D两点纵坐标相等，从而求出t值，代入（2）中的P点坐标即可得出结论．
解：（1）∵二次函数y=ax2图象过点A（8，8），
∴有8=82a=64a，解得a=，
∴这个二次函数的解析式y=x2．
∵点B为直线y=
x+4的图象与y轴的交点，
∴当x=0时，y=×0+4=4，
∴B点的坐标为（0，4）．
（2）∵P点在线段BA上，
∴P点坐标为（t，t+4）（0＜t＜8），
∵D点在二次函数图象上，且P、D横坐标相等，
∴D点坐标为（t，t2），
PD=h=t+4﹣t2=﹣t2+t+4（0＜t＜8）．
（3）∵当BD∥x轴时，B、D两点纵坐标相等，且B（0，4）
即4=t2，
解得t=4．
∴P点坐标为（4，4+2）．
