题目内容
【题目】按图填空, 并注明理由
已知: 如图, ∠1=∠2, ∠3=∠E. 求证: AD∥BE
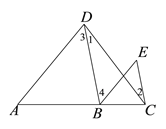
证明: ∵∠1 = ∠2 (已知)
∴ ∥ ( )
∴ ∠E = ∠ ( )
又∵ ∠E = ∠3 ( 已知 )
∴ ∠3 = ∠ ( 等量代换 )
∴ ∥ ( 内错角相等,两直线平行 )
【答案】EC;DB;内错角相等,两直线平行;两直线平行,内错角相等;4;等量代换;内错角相等,两直线平行
【解析】试题分析:首先根据∠1=∠2可得BD∥CE,再根据平行线的性质可得∠E=∠4,然后可证出∠3=∠4,再根据内错角相等,两直线平行可得AD∥BE.
试题解析:∵∠1=∠2(已知)
∴EC∥DB
(内错角相等,两直线平行)
∴∠E=∠4
(两直线平行,内错角相等)
又∵∠E=∠3(已知)
∴∠3=∠4 (等量代换)
∴AD∥BE.
(内错角相等,两直线平行)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目