��Ŀ����
��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣩����֪������y=x2+bx+c����A��4��0����B��1����3����
��1����b��c��ֵ����д���������ߵĶԳ���Ͷ������ꣻ
��2���������ߵĶԳ���Ϊֱ��l����P��m��n�������������ڵ�һ���ĵ㣬��E���P����ֱ��l�Գƣ���E���F����y��Գƣ����ı���OAPF�����Ϊ48�����P�����ꣻ
��3���ڣ�2���������£���M��ֱ��l������һ�㣬���ж�MP+MA�Ƿ������Сֵ�������ڣ���������Сֵ����Ӧ�ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��1��b=��4��c=0�������ߵĶԳ���Ϊx=2������Ϊ��2����4����
��2����P��������6��12����
��3�����ڣ���СֵΪ6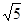 ��
��
���������������1���ô���ϵ�����Ϳ����b��c���ٽ�����ʽ��ɶ���ʽ���Ϳ����ˣ�
��2��������֪�����ɵ�E��4��m��n����F��m��4��n�����Ӷ��õ�PF=4�������ı���OAPF�����Ϊ48�������P�������꣬Ȼ����������ߵĽ���ʽ�Ϳ������P�����꣮
��3�����ݵ�E���P����ֱ��l�Գƿɵ�MP=ME������MP+MA=ME+MA�����ɡ�����֮���߶���̡��ɵ�AE�ij�����MP+MA����Сֵ�����ù��ɶ����Ϳɽ�����⣮
�����������1����������y=x2+bx+c����A��4��0����B��1����3����
��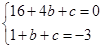 ��
��
��ã�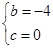 ��
��
��y=x2��4x=��x��2��2��4��
�������ߵĶԳ���Ϊx=2������Ϊ��2����4����
��2����ͼ1��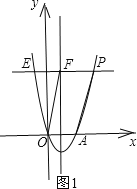
�ߵ�P��m��n�����E����ֱ��x=2�Գƣ�
���E��������4��m��n����
�ߵ�E���F����y��Գƣ�
���F��������m��4��n����
��PF=m����m��4��=4��
��PF=OA=4��
��PF��OA��
���ı���OAPF��ƽ���ı��Σ�
��S?OAPF=OA•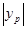 =4n=48��
=4n=48��
��n=12��
��m2��4m=n=12��
��ã�m1=6��m2=��2��
�ߵ�P�����������ڵ�һ���ĵ㣬
��m=6��
���P��������6��12����
��3������E��EH��x�ᣬ����ΪH����ͼ2��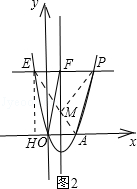
�ڣ�2���������£���P��6��12����E����2��12����
��AH=4������2��=6��EH=12��
��EH��x�ᣬ����EHA=90�㣬
��EA2=EH2+AH2=122+62=180��
��EA=6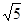 ��
��
�ߵ�E���P����ֱ��l�Գƣ�
��MP=ME��
��MP+MA=ME+MA��
���ݡ�����֮���߶���̡��ɵã�
����E��M��A����ʱ��MP+MA��С����Сֵ����EA�ij�����6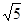 ��
��
���㣺1������ϵ������2���߶ε����ʣ�3�����ɶ�����4������x�ᡢy��ԳƵĵ�����꣮.

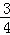 x��3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=��
x��3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=��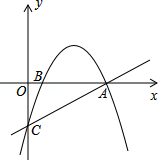

 �Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4��
�Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4�� ��
��
 ��c=2+b����������
��c=2+b����������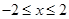 �����ϵ���Сֵ��-3����b��ֵ��
�����ϵ���Сֵ��-3����b��ֵ��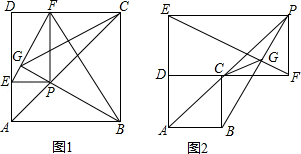

 ��b��c��Ϊ��������x�ύ��
��b��c��Ϊ��������x�ύ�� ���㣬��y�ύ�ڵ�
���㣬��y�ύ�ڵ� ��
��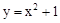 ����Сֵ�� ��
����Сֵ�� ��