题目内容
已知抛物线y=3ax2+2bx+c
(1)若a=b=1,c=-1求该抛物线与x轴的交点坐标;
(2)若a= ,c=2+b且抛物线在
,c=2+b且抛物线在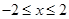 区间上的最小值是-3,求b的值;
区间上的最小值是-3,求b的值;
(3)若a+b+c=1,是否存在实数x,使得相应的y的值为1,请说明理由.
(1)该抛物线与x轴公共点的坐标是:(﹣1,0)和( ,0);
,0);
(2)b=3或b=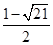 ;
;
(3)存在两个不同实数x,使得相应y=1.
解析试题分析:(1)直接将a=b=1,c=﹣1代入求出即可;
(2)利用当x=﹣b<﹣2时,即b>2,此时﹣3=(﹣2)2+2×(﹣2)b+b+2;当x=﹣b>2时,即b<﹣2,则有抛物线在x=2时取最小值为﹣3,此时﹣3=22+2×2b+b+2;当﹣2≤﹣b≤2时,即﹣2≤b≤2,则有抛物线在x=﹣b时,取最小值为﹣3,分别求出符合题意的答案即可;
(3)由y=1得3ax2+2bx+c=1,则△=4b2﹣12a(c﹣1),求出其符号得出答案即可.
试题解析:(1)当a=b=1,c=﹣1时,抛物线为:y=3x2+2x﹣1,
∵方程3x2+2x﹣1=0的两个根为:x1=﹣1,x2= .
.
∴该抛物线与x轴公共点的坐标是:(﹣1,0)和( ,0);
,0);
(2)a= ,c﹣b=2,则抛物线可化为:y=x2+2bx+b+2,
,c﹣b=2,则抛物线可化为:y=x2+2bx+b+2,
其对称轴为:x=﹣b,
当x=﹣b<﹣2时,即b>2,则有抛物线在x=﹣2时取最小值为﹣3,
此时﹣3=(﹣2)2+2×(﹣2)b+b+2,
解得:b=3,符合题意,
当x=﹣b>2时,即b<﹣2,则有抛物线在x=2时取最小值为﹣3,此时﹣3=22+2×2b+b+2,
解得:b=﹣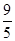 ,不合题意,舍去.
,不合题意,舍去.
当﹣2≤﹣b≤2时,即﹣2≤b≤2,则有抛物线在x=﹣b时,取最小值为﹣3,
此时﹣3=(﹣b)2+2×(﹣b)b+b+2,
化简得:b2﹣b﹣5=0,
解得:b1=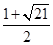 (不合题意,舍去),b2=
(不合题意,舍去),b2=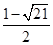 .
.
综上:b=3或b=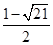 ;
;
(3)由y=1得3ax2+2bx+c=1,
△=4b2﹣12a(c﹣1),
=4b2﹣12a(﹣a﹣b),
=4b2+12ab+12a2,
=4(b2+3ab+3a2),
=4[(b+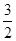 a)2+
a)2+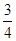 a2],
a2],
∵a≠0,△>0,
所以方程3ax2+2bx+c=1有两个不相等实数根,
即存在两个不同实数x,使得相应y=1.
考点:二次函数综合题.

 名校课堂系列答案
名校课堂系列答案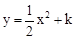 与扇形OAB的边界总有两个公共点,则实数k的取值范围是
与扇形OAB的边界总有两个公共点,则实数k的取值范围是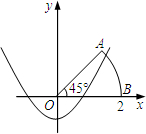
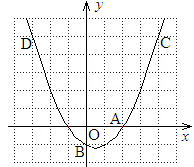
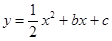 与x轴交于A,B两点,对称轴为直线
与x轴交于A,B两点,对称轴为直线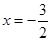 ,直线AD交抛物线于点D(2,3).
,直线AD交抛物线于点D(2,3).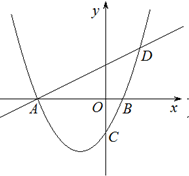


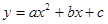 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;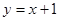 ,并写出当
,并写出当