题目内容
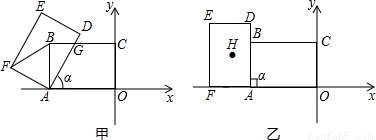
在平面直角坐标系xOy中,把矩形AOCB绕点A逆时针旋转α角,得到矩形ADEF,设AD与BC相交于点G,且A(-9,0),C(0,6),如图甲.(1)当α=60°时,请猜测△ABF的形状,并对你的猜测加以证明.
(2)当GA=GC时,求直线AD的解析式.
(3)当α=90°时,如图乙.请探究:经过点F,且以点B为顶点的抛物线,是否经过矩形ADEF的对称中心H,并说明理由.
【答案】分析:(1)根据旋转的知识可得AB=AF,根据∠BAF=60°可得∴△ABF为等边三角形;
(2)利用△AGB为直角三角形,根据勾股定理可得CG的长,也求得了G的坐标,利用点A、G的坐标可得所求的直线解析式;
(3)易得F坐标,利用顶点式可得经过点F,且以点B为顶点的抛物线,易得H的坐标,把横坐标代入所得函数解析式,看是否等于纵坐标即可.
解答:解:(1)矩形ADEF是矩形AOCB绕点A逆时针旋转α=60°角而得,
∴AF=AB.
又∵∠FAB+∠BAG=∠α+∠BAG=90°,
即∠FAB=∠α=60°.
∴△ABF为等边三角形.
(2)设CG=x,则BG=9-x,而AB=OC=6,GA=GC.
∴在Rt△AGB中,(9-x)2+62=x2.
解之得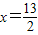 .
.
∴点G坐标为(-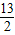 ,6).
,6).
设直线AD的解析式为y=kx+b,
∵AD经过A(-9,0),G(-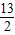 ,6),
,6),
∴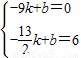 ,
,
解之得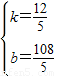 .
.
∴所求直线AD的解析式为: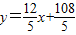 .
.
(3)据题意,∵抛物线顶点B(-9,6),又过点F(-15,0),
∴设抛物线解析式为y=a(x+9)2+6.
∴a(-15+9)2+6=0,即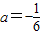 .
.
∴抛物线的解析式为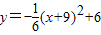 .
.
又∵点H是矩形ADEF的对称中心,
∴H(-12, ).
).
将x=-12代入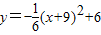 ,得
,得 .
.
∴抛物线要经过矩形ADEF的对称中心H.
点评:综合考查二次函数的应用;用到的知识点为:有一个角等于60°的等腰三角形是等边三角形;二次函数的顶点式可表示为:y=a(x-h)2+k.利用勾股定理得到CG的长是解决本题的突破点.
(2)利用△AGB为直角三角形,根据勾股定理可得CG的长,也求得了G的坐标,利用点A、G的坐标可得所求的直线解析式;
(3)易得F坐标,利用顶点式可得经过点F,且以点B为顶点的抛物线,易得H的坐标,把横坐标代入所得函数解析式,看是否等于纵坐标即可.
解答:解:(1)矩形ADEF是矩形AOCB绕点A逆时针旋转α=60°角而得,
∴AF=AB.
又∵∠FAB+∠BAG=∠α+∠BAG=90°,
即∠FAB=∠α=60°.
∴△ABF为等边三角形.
(2)设CG=x,则BG=9-x,而AB=OC=6,GA=GC.
∴在Rt△AGB中,(9-x)2+62=x2.
解之得
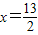 .
.∴点G坐标为(-
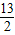 ,6).
,6).设直线AD的解析式为y=kx+b,
∵AD经过A(-9,0),G(-
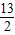 ,6),
,6),∴
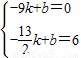 ,
,解之得
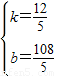 .
.∴所求直线AD的解析式为:
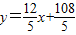 .
.(3)据题意,∵抛物线顶点B(-9,6),又过点F(-15,0),
∴设抛物线解析式为y=a(x+9)2+6.
∴a(-15+9)2+6=0,即
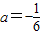 .
.∴抛物线的解析式为
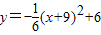 .
.又∵点H是矩形ADEF的对称中心,
∴H(-12,
 ).
).将x=-12代入
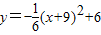 ,得
,得 .
.∴抛物线要经过矩形ADEF的对称中心H.
点评:综合考查二次函数的应用;用到的知识点为:有一个角等于60°的等腰三角形是等边三角形;二次函数的顶点式可表示为:y=a(x-h)2+k.利用勾股定理得到CG的长是解决本题的突破点.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为