Question

【题目】已知：如图，∠A=90°，BC∥AD，AB=6cm，点P从A出发沿射线AD运动，速度是每秒1cm，点R从点B出发沿射线BC运动，速度是每秒2cm，点Q在点P的右侧，且PQ=10cm，时间为t秒；

求：（1）△PQR的面积；

（2）当t=1秒时，求PR的长；

（3）当t为何值时，△PQR是等腰三角形？

Answer 1

【答案】（1）30cm2；（2）；（3）当t=2或5或8或18时，△PQR是等腰三角形.

【解析】

（1）由三角形面积=底和高乘积的一半即可求得；

（2）过R作RM⊥AD于点M，证得四边形ABRM是矩形，再由勾股定理可求得PR的值；

（3）分情况讨论即可.

（1）S△PQR==30cm2；

（2）当t=1时，BR==2，AP=1，

如图：过R作RM⊥AD于点M，

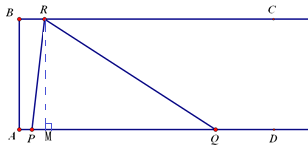
∵∠A=90°，BC∥AD，

∴∠B=90，

∴四边形ABRM是矩形，

∴PM=AB=6，AM=BR=2，PM=AM-AP=1，

∴PR=；

（3）分4种情况：

①PQ=QR时，如图：

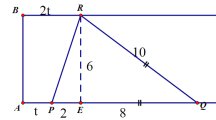
可得BR-AP=2，2t-t=2，

解得t=2；

②PR=RQ时，如图：

可得2t-t=5，

解得t=5；

③PR=PQ时，如图：

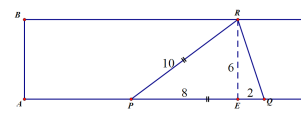
可得2t-t=8，

解得t=8；

④PQ=QR时，如图：

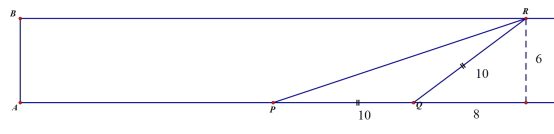
可得2t-t=18，t=18.

综上所述，当t=2或5或8或18时，△PQR是等腰三角形.