题目内容
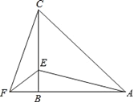
【题目】如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.
(1)求证:AB⊥BE.
(2)求证:AE=2CN.

【答案】见解析
【解析】
(1)证明△DCA与△ECB全等,再利用全等三角形的性质证明即可;
(2)延长CN至点K,使NK=CN,连接DK,利用已知条件证明△DNK≌△BNC,所以可得DK=BC=AC,∠KDC+∠DCB=180°,又因为∠DCK=∠ACE,DK=AC,CD=CE,由三角形的全等可得AE=CK,所以AE=2CN.
证明:(1)∵CE⊥CD,∠ACB=90°,
∴∠DCE=∠ACB=90°,
∴∠DCA+∠ACE=∠BCE+∠ACE,
∴∠DCA=∠BCE,
在△DCA与△ECB中,
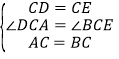 ,
,
∴△DCA≌△ECB(SAS),
∴∠CDA=∠CEB,∠DAC=∠EBC=135°,
∴∠ABE=∠CBE-∠ABC=135°-45°=90°,
∴AB⊥BE;
(2)延长CN至点K,使NK=CN,连接DK.
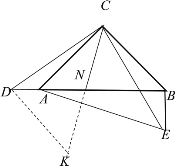
∵∠DCA+∠ACE=90°,∠BCE+∠ACE=90°,
∴∠DCB+∠ACE=180°,
∴∠KDN=∠CBN,
∴DK∥BC,
∵在△DNK与△BNC中,
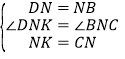
∴△DNK≌△BNC,
∴DK=BC=AC,
∴∠KDC+∠DCB=180°,
∵∠DCK=∠ACE,
又∵DK=AC,CD=CE,
∵△KDC≌△ACE,
∴AE=CK,
∴AE=2CN.

练习册系列答案
相关题目