题目内容
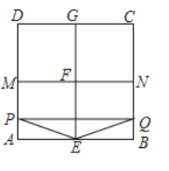
【题目】如图,在![]() 的正方形网格中,动点
的正方形网格中,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点匀速出发,以每秒1个单位长度的速度沿网格线运动至格点
两点匀速出发,以每秒1个单位长度的速度沿网格线运动至格点![]() 停止.动点
停止.动点![]() 的运动路线为:
的运动路线为:![]() ;动点
;动点![]() 的运动路线为:
的运动路线为:![]() ,连接
,连接![]() 、
、![]() .设动点
.设动点![]() 运动时间为
运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
A.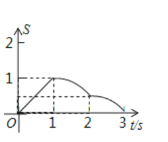 B.
B.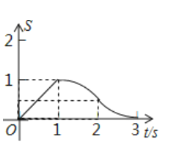
C.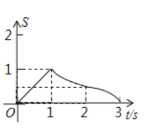 D.
D.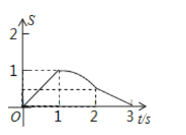
【答案】A
【解析】
分0≤t≤1、1<t<2、2≤t≤3三种情况,分别求出函数表达式即可求解.
①0≤t≤1时,如图,
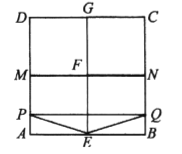
S=![]() PQ
PQ![]() AP=t,
AP=t,
当t=1时,S=1,
该函数为一次函数;
②1<t<2时,如图,建立如图所示的坐标系,
则点P、Q的坐标分别为(t-1,1)、(2,t),设直线PQ交GE于点H,
设直线PQ的表达式为:![]() ,则
,则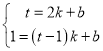 ,
,
解得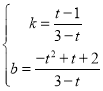 ,
,
故直线PQ的表达式为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴ ;
;
该函数为开口向下的抛物线;
③当2≤t≤3时,如图,
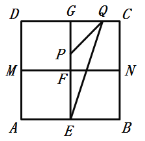
PF=t-2,GQ = 3- t,
∴PE= t-2+1 =t-1,
同理可得:S=![]() PE
PE![]() GQ=
GQ=![]() (t-1)( 3- t)=
(t-1)( 3- t)=![]() ;
;
该函数为开口向下的抛物线;
故选:A.

【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.
【题目】已知甲、乙两辆汽车分别从![]() 、
、![]() 两地同时匀速出发,甲车开往
两地同时匀速出发,甲车开往![]() 地,乙车开往
地,乙车开往![]() 地,设甲、乙两车距
地,设甲、乙两车距![]() 地的路程分别为
地的路程分别为![]() 、
、![]() (单位:
(单位:![]() ),甲车的行驶时间为
),甲车的行驶时间为![]() (单位:
(单位:![]() ).若甲车的速度为
).若甲车的速度为![]() ,
,![]() 与
与![]() 之间的对应关系如下表:
之间的对应关系如下表:
| 2 | 5 |
| 560 | 320 |
(1)分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;(不写
之间的函数关系式;(不写![]() 的取值范围)
的取值范围)
(2)当![]() 为何值时,甲、乙两辆汽车相遇?
为何值时,甲、乙两辆汽车相遇?
(3)当两车距离小于![]() 时,求
时,求![]() 的取值范围.
的取值范围.