题目内容
已知反比例函数y1=
的图象与一次函数y2=kx+m的图象相交于A(2,1).
(1)分别求出这两个函数的解析式,并在同一坐标系内画出它们的大致图象;
(2)试判断P(-1,5)关于x轴的对称点Q是否在一次函数y2=kx+m的图象上,若在请求出S△APQ;若不在,请求出直线AQ的解析式;
(3)若一次函数的图象与反比例函数的图象的另一个交点为B,且B点的纵坐标为-4,请根据图象回答:①当x取何值时,y1>y2;②当x取何值时,y1•y2>0.

| k | x |
(1)分别求出这两个函数的解析式,并在同一坐标系内画出它们的大致图象;
(2)试判断P(-1,5)关于x轴的对称点Q是否在一次函数y2=kx+m的图象上,若在请求出S△APQ;若不在,请求出直线AQ的解析式;
(3)若一次函数的图象与反比例函数的图象的另一个交点为B,且B点的纵坐标为-4,请根据图象回答:①当x取何值时,y1>y2;②当x取何值时,y1•y2>0.

分析:(1)把A(2,1)代入反比例函数y1=
与一次函数y2=kx+m的解析式即可求出k、m的值,可得到解析式,再画出函数图象即可;
(2)首先根据关于x轴对称的点的坐标特点写出Q点的坐标,再根据解析式计算当x=-1时,y的值,即可判断出Q点是否在一次函数图象上;根据P、Q、A点坐标可算出△APQ的面积;
(3)首先计算出b点坐标,再结合图象可以直接写出答案.
| k |
| x |
(2)首先根据关于x轴对称的点的坐标特点写出Q点的坐标,再根据解析式计算当x=-1时,y的值,即可判断出Q点是否在一次函数图象上;根据P、Q、A点坐标可算出△APQ的面积;
(3)首先计算出b点坐标,再结合图象可以直接写出答案.
解答: 解:(1)∵反比例函数y1=
解:(1)∵反比例函数y1=
的图象与一次函数y2=kx+m的图象相交于A(2,1),
∴k=2×1=2,k×2+m=1,
∴k=2,m=-3,
∴y1=
,y2=2x-3;
(2)∵点P(-1,5)关于x轴对称点Q的坐标为(-1,-5)
∴当x=-1时,y=2×(-1)-3=-5
∴点Q在直线y2=2x-3上,
∴S△APQ=
×10×3=15;
(3)∵B点的纵坐标为-4,
∴-4x=2,
x=-
,
∴双曲线与直线的两个交点A(2,1)、B(-
,-4),
①当x<-
或0<x<2时,y1>y2,
②∵直线AB与x轴交于点(
,0),
∴当x>
或x<0时,y1•y2>0.
 解:(1)∵反比例函数y1=
解:(1)∵反比例函数y1=| k |
| x |
∴k=2×1=2,k×2+m=1,
∴k=2,m=-3,
∴y1=
| 2 |
| x |
(2)∵点P(-1,5)关于x轴对称点Q的坐标为(-1,-5)
∴当x=-1时,y=2×(-1)-3=-5
∴点Q在直线y2=2x-3上,
∴S△APQ=
| 1 |
| 2 |
(3)∵B点的纵坐标为-4,
∴-4x=2,
x=-
| 1 |
| 2 |
∴双曲线与直线的两个交点A(2,1)、B(-
| 1 |
| 2 |
①当x<-
| 1 |
| 2 |
②∵直线AB与x轴交于点(
| 3 |
| 2 |
∴当x>
| 3 |
| 2 |
点评:此题主要考查了待定系数法求反比例函数与一次函数解析式,画反比例函数与一次函数图象,判断点是否在函数图象上,利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
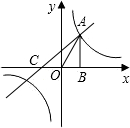 为1.过点A作AB⊥x轴于点B,△AOB的面积1.
为1.过点A作AB⊥x轴于点B,△AOB的面积1.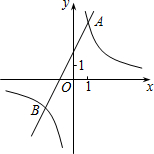 已知反比例函数y1=
已知反比例函数y1= 如图,已知反比例函数
如图,已知反比例函数 已知反比例函数
已知反比例函数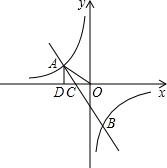 的横坐标为
的横坐标为