题目内容
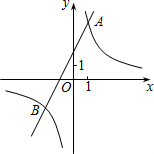 已知反比例函数y1=
已知反比例函数y1=| k | x |
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
分析:(1)先根据点A的坐标求出反比例函数的解析式为y1=
,再求出B的坐标是(-2,-2),利用待定系数法求一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出一次函数的值小于反比例函数的值x的取值范围x<-2 或0<x<1.
(3)根据坐标与线段的转换可得出:AC、BD的长,然后根据三角形的面积公式即可求出答案.
| 4 |
| x |
(2)当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出一次函数的值小于反比例函数的值x的取值范围x<-2 或0<x<1.
(3)根据坐标与线段的转换可得出:AC、BD的长,然后根据三角形的面积公式即可求出答案.
解答:解:(1)∵函数y1=
的图象过点A(1,4),即4=
,
∴k=4,即y1=
,
又∵点B(m,-2)在y1=
上,
∴m=-2,
∴B(-2,-2),
又∵一次函数y2=ax+b过A、B两点,
即
,
解之得
.
∴y2=2x+2.
综上可得y1=
,y2=2x+2.
(2)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
如图所示:当x<-2 或0<x<1时y1>y2.
(3)
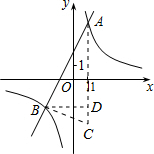
由图形及题意可得:AC=8,BD=3,
∴△ABC的面积S△ABC=
AC×BD=
×8×3=12.
| k |
| x |
| k |
| 1 |
∴k=4,即y1=
| 4 |
| x |
又∵点B(m,-2)在y1=
| 4 |
| x |
∴m=-2,
∴B(-2,-2),
又∵一次函数y2=ax+b过A、B两点,
即
|
解之得
|
∴y2=2x+2.
综上可得y1=
| 4 |
| x |
(2)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
如图所示:当x<-2 或0<x<1时y1>y2.
(3)
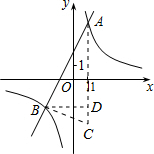
由图形及题意可得:AC=8,BD=3,
∴△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式.以及三角形面积的求法,这里体现了数形结合的思想.

练习册系列答案
相关题目
 为1.过点A作AB⊥x轴于点B,△AOB的面积1.
为1.过点A作AB⊥x轴于点B,△AOB的面积1. 如图,已知反比例函数
如图,已知反比例函数 已知反比例函数
已知反比例函数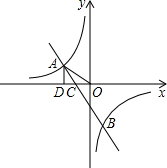 的横坐标为
的横坐标为