题目内容
【题目】已知O为直线AB上的一点,射线OA表示正北方向,∠COE=90°,射线OF平分∠AOE.
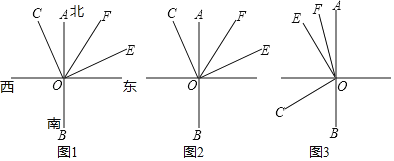
(1)如图1,若∠AOE=70°,则∠COF的度数是 ;
(2)若将∠COE绕点O旋转至图2的位置,试判断∠COF和∠BOE之间的数量关系,并证明你的证明;
(3)若将∠COE绕点O旋转至图3的位置,直接写出2∠COF+∠BOE的度数是 .
【答案】(1)55°;(2)∠COF=![]() ∠BOE,理由见解析;(3)360°
∠BOE,理由见解析;(3)360°
【解析】
(1)可以知道∠COF=∠COE﹣∠FOE,所以只要求出∠FOE即可.注意到OF平分∠AOE,∠AOE=70°,则可求出∠FOE=35°
(2)设∠BOE=α,则∠AOE=180°﹣α,求出∠FOE,代入∠COF=∠COE﹣∠FOE即可
(3)可先设∠AOE=2β,则∠EOF=β,通过有计算出,∠COF=90°+β,∠BOE=180°﹣2β代入2∠COF+∠BOE即可求解
解:(1)∵OF平分∠AOE,∠AOE=70°
∴∠FOE=∠AOF=![]() ∠AOE=
∠AOE=![]() ×70°=35°
×70°=35°
∴∠COF=∠COE﹣∠FOE=90°﹣35°=55°
故答案为:55°
(2)∠COF=![]() ∠BOE,理由如下:
∠BOE,理由如下:
设∠BOE=α,则∠AOE=180°﹣α,∠EOF=![]() ∠AOE=
∠AOE=![]() (180°﹣α),
(180°﹣α),
∴∠COF=90°﹣![]() (180°﹣α)=
(180°﹣α)=![]() α,
α,
∴∠COF=![]() ∠BOE
∠BOE
(3)设∠AOE=2β,则∠EOF=β,
∴∠COF=90°+β,∠BOE=180°﹣2β
∴2∠COF+∠BOE=2(90°+β)+180°﹣2β=360°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目