题目内容
【题目】已知二次函数
，完成下列各题：
将函数关系式用配方法化为
的形式，并写出它的顶点坐标、对称轴．
求出它的图象与坐标轴的交点坐标．
在直角坐标系中，画出它的图象．
根据图象说明：当
为何值时，
；当为何值时，
．
【答案】（1）
，顶点（2,9），对称轴x=2
（2）与x轴交点（5,0）（-1,0），与y轴交点（0,5）
（3）图略
（4）当-1<x<5时，y>0,当x>5或x<-1时，y<0。
【解析】
试题（1）用配方法整理，进而得出顶点坐标和对称轴即可；
（2）让函数值为0，求得一元二次方程的两个解即为这个二次函数的图象与坐标轴的交点的横坐标，让x=0，可求得抛物线与y轴的交点坐标；找到与y轴的交点，x轴的交点，对称轴，即可画出大致图象；
（3）由（1）和（2）中的条件即可画出它的图象；
（4）分别找到x轴上方和下方函数图象所对应的自变量的取值即可．
试题解析：（1）y=-x2+4x+5=-（x2-4x+4）+9=-（x-2）2+9；
故它的顶点坐标为（2，9）、对称轴为：x=2；（2）图象与x轴相交是y=0，则：
0=-（x-2）2+9，
解得x1=5，x2=-1，
∴这个二次函数的图象与x轴的交点坐标为（5，0），（-1，0）；
当x=0时，y=5，
∴与y轴的交点坐标为（0，5）；
（3）画出大致图象为
；
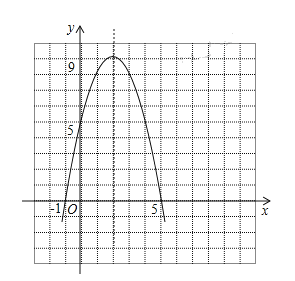4）-1＜x＜5时 y＞0；x＜-1或x＞5时 y＜0．
练习册系列答案
阅读快车系列答案
相关题目
