Question

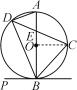
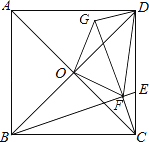
【题目】如图，正方形ABCD的边长为12，点O为对角线AC、BD的交点，点E在CD上，tan∠CBE= ，过点C作CF⊥BE，垂足为F，连接OF，将△OCF绕着点O逆时针旋转90°得到△ODG，连接FG、FD，则△DFG的面积是________．

Answer 1

【答案】

【解析】

根据tan∠CBE=可得CE的长度，利用勾股定理可求出BE的长度，利用面积公式可求出CF的长度，根据正方形的性质及旋转的性质可得∠BCF=∠CGD，CF=DG，通过证明△BCF≌△CDG，可得∠FGD=90°，利用勾股定理可求出CG的长，进而可得GF的长，根据三角形面积公式即可得答案.

∵tan∠CBE=；BC=12，

∴CE=12tan∠CBE=4，

∴BE==4，

∵CF⊥BE，

∴BC×CE=BE×CF，

∴CF==，

∴DG=，

∵△OCF绕着点O逆时针旋转90°得到△ODG，

∴∠OCF=∠ODG，CF=DG

∵AC、BD是正方形ABCD的对角线，

∴∠ACB=∠BDC=45°，

∴∠ACB+∠OCF=∠BDC+∠ODG，即∠BCF=∠CDG，

又∵BC=CD，CF=DG，

∴△BCF≌△CDG，

∴∠BFC=∠CDG=90°，

∴CG===；

∴GF=CG-CF=-=，

∴S△DFG=GFDG= =，

故答案为：