题目内容
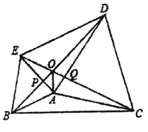
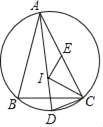
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
【答案】4
【解析】
由已知条件可得到ID=BD=DC,可得I、B、C三点在以D点位圆心的圆上,过点D做DF⊥IC与点F,可得四边形EIDF为平行四边形,可得IE=DF,即可求出IE的长.
解:
如图:I为△ABC的内心,可得∠BAD=∠CAD,![]() BD=CD,
BD=CD,
又∠DIC=∠DAC+∠ACI,∠ICD=∠ICB+∠BCD
其中∠DAC=∠BAD=∠BCD,∠ACI=∠ICB,
![]() ∠DIC=∠ICD
∠DIC=∠ICD
![]() ID=CD,
ID=CD, ![]() ID=BD=DC=5, 可得AI=2CD=10
ID=BD=DC=5, 可得AI=2CD=10
![]() 可得I、B、C三点在以D点位圆心的圆上,过点D做DF⊥IC与点F,
可得I、B、C三点在以D点位圆心的圆上,过点D做DF⊥IC与点F,
可得IF=FC(垂经定理),
在RT△IFD中,![]() ,
,
又在△AIC中,AE=EC, IF=FC,
![]() EF为△AIC的中位线,
EF为△AIC的中位线,
![]() EF∥AD,即EF∥ID, 且EF=
EF∥AD,即EF∥ID, 且EF=![]() =5=ID,
=5=ID,
![]() 四边形EIDF为平行四边形,可得IE=DF=4,
四边形EIDF为平行四边形,可得IE=DF=4,
故答案:4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目