题目内容
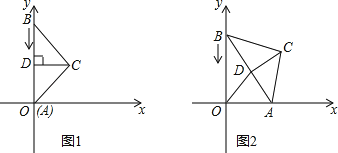
【题目】如图，已知直线l∥AB，l与AB之间的距离为2．C、D是直线l上两个动点（点C在D点的左侧），且AB=CD=5．连接AC、BC、BD，将△ABC沿BC折叠得到△A′BC．下列说法：①四边形ABCD的面积始终为10；②当A′与D重合时，四边形ABDC是菱形；③当A′与D不重合时，连接A′、D，则∠CA′D+∠BCA′=180°；④若以A′、C、B、D为顶点的四边形为矩形，则此矩形相邻两边之和为3
或7．其中正确的是（ ）
A. ①②④ B. ①③④ C. ①②③ D. ①②③④
【答案】D
【解析】分析：①根据平行四边形的判定方法可得到四边形ABCD为平行四边形，然后根据平行四边形的面积公式计算；②根据折叠的性质得到AC=CD，然后根据菱形的判定方法可判断四边形ABDC是菱形；③连结A′D，根据折叠性质和平行四边形的性质得到CA′=CA=BD，AB=CD=A′B，∠1=∠CBA=∠2，可证明△A′CD≌△A′BD，则∠3=∠4，然后利用三角形内角和定理得到得到∠1=∠4，则根据平行线的判定得到A′D∥BC；④讨论：当∠CBD=90°，则∠BCA=90°，由于S△A1CB=S△ABC=5，则S矩形A′CBD=10，根据勾股定理和完全平方公式进行计算；当∠BCD=90°，则∠CBA=90°，易得BC=2，而CD=5，于是得到结论．
详解：①∵AB=CD=5，AB∥CD，∴四边形ABCD为平行四边形，
∴四边形ABDC的面积=2×5=10；故①正确；
②∵四边形ABDC是平行四边形，∵A′与D重合时，∴AC=CD，
∵四边形ABDC是平行四边形，∴四边形ABDC是菱形；故②正确；
③连结A′D，如图，∵△ABC沿BC折叠得到△A′BC，
∴CA′=CA=BD，AB=CD=A′B， ∴△A′CD≌△A′BD（SSS），
∴∠3=∠4， 又∵∠1=∠CBA=∠2， ∴∠1+∠2=∠3+∠4， ∴∠1=∠4，
∴A′D∥BC， ∴∠CA′D+∠BCA′=180°；故③正确；
④设矩形的边长分别为a，b，当∠CBD=90°，∵四边形ABDC是平行四边形，
∴∠BCA=90°， ∴S△A′CB=S△ABC=5， ∴S矩形A′CBD=10，即ab=10， 而BA′=BA=5，
∴a2+b2=25， ∴（a+b）2=a2+b2+2ab=45， ∴a+b=
；
当∠BCD=90°时， ∵四边形ABDC是平行四边形， ∴∠CBA=90°， ∴BC=2，
而CD=5， ∴（a+b）2=（2+5）2=49， ∴a+b=7，
∴此矩形相邻两边之和为或7，故④正确． 故选D．
