题目内容
【题目】操作与证明: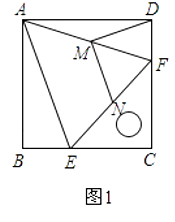
如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是:;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.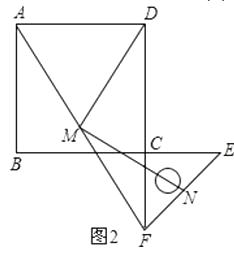
【答案】
(1)证明:如图1中,
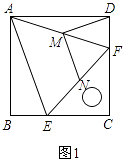
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠ADF=90°,
∵CE=CF,
∴BE=DF,
∴△ABE≌△ADF,
∴AE=AF,
∴△AEF是等腰三角形
(2)MN=DM,MN⊥DM
(3)解:结论仍然成立.
理由:如图2中,连接AE,设AE交DM于O,交CD于G.
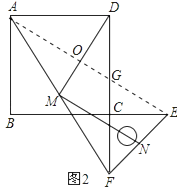
∵AB=AD,BE=DF,∠ABE=∠ADF=90°,
∴△ABE≌△ADF,
∴AF=AE,∠AFD=∠AEB,
∵AM=MF,FN=EN,
∴MN= ![]() AE,DM=
AE,DM= ![]() AF,
AF,
∴MN=DM,
∵DM=MF=AM,
∴∠MDF=∠MFD=∠AEB,
∵∠DGO=∠CGE,∠ODG=∠CEG,
∴∠DOG=∠ECG=90°,
∵NM∥AE,
∴∠DOG=∠DMN=90°,
∴MN⊥DM,MN=DM.
【解析】(2)解:结论:DM=MN,DM┴MN
证明:∵AM=FM,FN=EN,
∴MN= ![]() AE,DM=
AE,DM= ![]() AF,
AF,
∵AE=AF,
∴MN=DM,
∵∠ADF=90°,AM=MF,
∴MD=MA=MF,
∴∠MAD=∠ADM,
∵∠DMF=∠MAD+∠ADM=2∠DAM,
∵△ABE≌△ADF,
∴∠BAE=∠DAF,
∵∠EAF+2∠DAM=90°,
∵MN∥AE,
∴∠NMF=∠EAF,
∴∠NMF+∠DMF=90°,
∴DM⊥MN.
∴MN=DM,MN⊥DM.
所以答案是MN=DM,MN⊥DM.
(1)欲证明△AEF是等腰三角形,只要证明△ABE≌△ADF即可;(2)结论:DM=MN,DM┴MN.利用三角形中位线定理.直角三角形斜边中线定理即可解决问题.(3)结论不变.证明方法类似.

 优学名师名题系列答案
优学名师名题系列答案