题目内容
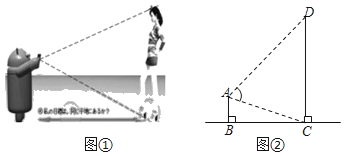
【题目】如图，某“拓展训练营”的一个自行车爬坡项目有两条不同路线，路线一：从C到B，路线二：从D到A，AB为垂直升降梯．其中BC的坡度为i=1：2，BC=12
米，CD＝8米，∠D=
（其中A，B，C，D均在同一平面内），则垂直升降梯AB的高度约为（精确到0.1米）（ ）（参考数据：tan36°≈0.73，cos36°≈0.81，sin36°≈0.59）
A.8.6B.11.4C.13.9D.23.4
【答案】B
【解析】
根据勾股定理可得CE，BE的长，根据正切函数可得AE的长，再根据线段的和差即可求得答案．
解：如图，延长AB和DC相交于点E，
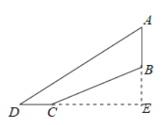
由斜坡BC的坡度为i=1：2，得BE：CE=1：2．
设BE=x米，CE=2x米．
在Rt△BCE中，由勾股定理，得
，
即
，
解得x=12，
∵BE=12米，CE=24米，
∴DE=DC+CE=8+24=32（米），
由tan36°≈0.73，得
=0.73，
解得AE=0.73×32=23.36（米）．
由线段的和差，得AB=AE-BE=23.36-12=11.36≈11.4（米）.
故选：B．
练习册系列答案
相关题目
