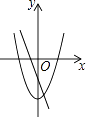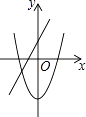题目内容
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，以下四个结论：①a＞0；②c＞0；③b2﹣4ac＞0；④﹣ 
＜0，正确的是（ ）
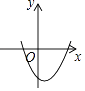
A.①②
B.②④
C.①③
D.③④
【答案】C
【解析】①∵抛物线开口向上，
∴a＞0，结论①正确；
②∵抛物线与y轴的交点在y轴负半轴，
∴c＜0，结论②错误；
③∵抛物线与x轴有两个交点，
∴△=b2﹣4ac＞0，结论③正确；
④∵抛物线的对称轴在y轴右侧，
∴﹣ 
＞0，结论④错误．
所以答案是：C．
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
练习册系列答案
相关题目
【题目】某商场计划用
元从厂家购进
台新型电子产品，已知该厂家生产甲、乙、丙三种不同型号的电子产品，设甲、乙型设备应各买入
台，其中每台的价格、销售获利如下表：
甲型 | 乙型 | 丙型 | |
价格（元/台） |
|
|
|
销售获利（元/台） |
|
|
|
购买丙型设备 台(用含
的代数式表示) ；
若商场同时购进三种不同型号的电子产品(每种型号至少有一台)，恰好用了元，则商场有哪几种购进方案?
在第题的基础上，为了使销售时获利最多，应选择哪种购进方案?此时获利为多少?
