题目内容
【题目】阅读下面材料:
材料一:分解因式是将一个多项式化为若干个整式积的形式的变形,“十字相乘法”可把某些二次三项式分解为两个一次式的乘积,具体做法如下:对关于![]() ,
,![]() 的二次三项式
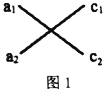
的二次三项式![]() ,如图1,将
,如图1,将![]() 项系数
项系数![]() ,作为第一列,
,作为第一列,![]() 项系数
项系数![]() ,作为第二列,若
,作为第二列,若![]() 恰好等于
恰好等于![]() 项的系数
项的系数![]() ,那么
,那么![]() 可直接分解因式为:
可直接分解因式为:![]()
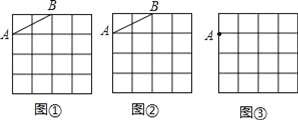
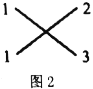
示例1:分解因式:![]()
解:如图2,其中![]() ,
,![]() ,而
,而![]() ;
;
∴![]() ;
;
示例2:分解因式:![]() .
.
解:如图3,其中![]() ,
,![]() ,而
,而![]() ;
;
∴![]() ;
;

材料二:关于![]() ,
,![]() 的二次多项式
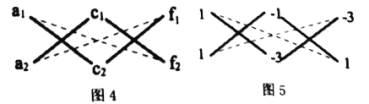
的二次多项式![]() 也可以用“十字相乘法”分解为两个一次式的乘积.如图4,将
也可以用“十字相乘法”分解为两个一次式的乘积.如图4,将![]() 作为一列,
作为一列,![]() 作为第二列,
作为第二列,![]() 作为第三列,若
作为第三列,若![]() ,
,![]() ,
,![]() ,即第1、2列,第1、3列和第2、3列都满足十字相乘规则,则原式分解因式的结果为:
,即第1、2列,第1、3列和第2、3列都满足十字相乘规则,则原式分解因式的结果为:![]() ;
;
示例3:分解因式:![]() .
.
解:如图5,其中![]() ,
,![]() ,
,![]() ;
;
满足![]() ,
,![]() ;
;
∴![]()
请根据上述材料,完成下列问题:
(1)分解因式:![]() ;
;![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 均为整数,且关于
均为整数,且关于![]() ,
,![]() 的二次多项式
的二次多项式![]() 可用“十字相乘法”分解为两个一次式的乘积,求出
可用“十字相乘法”分解为两个一次式的乘积,求出![]() 的值,并求出关于
的值,并求出关于![]() ,
,![]() 的方程
的方程![]() 的整数解.
的整数解.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() 和
和![]()
【解析】
(1)①直接用十字相乘法分解因式;②把某个字母看成常数用十字相乘法分解即可;
(2)用十字相乘法把能分解的集中情况全部列出求出m值.
解:(1)①1=1×1,2=1×2,3=1×1+1×2,
∴原式=![]() ;
;
②1=1×1,6=(-2)×(-3),-20=5×(-4)
满足(-5)=1×(-2)+1×(-3),1=1×5+1×(-4),2=(-2)×5+(-3)×(-4)
∴原式=![]() ;
;
(2)①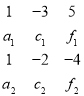
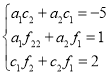
②![]()
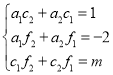
![]()
![]()
∴![]()
![]()
∴![]()
当![]() 时,
时,![]()
![]() 或
或![]() ,
,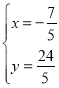 (舍),
(舍),![]()
当![]() 时,
时,![]()
![]() 或
或![]() ,
,![]() 或
或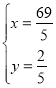 (舍)
(舍)
综上所述,方程![]() 的整数解有
的整数解有![]() 和
和![]() ;
;
方法二:![]()
![]()
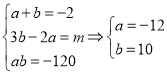 或
或![]() .
.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?