题目内容
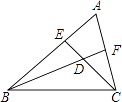
【题目】如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD，若DE=6，∠BAC+∠EAD=180°，则弦BC的长等于（ ）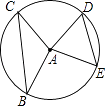
A.8
B.10
C.11
D.12
【答案】A
【解析】作AH⊥BC于H，作直径CF，连结BF，如图，
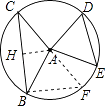
∵∠BAC+∠EAD=180°，
而∠BAC+∠BAF=180°，
∴∠DAE=∠BAF，
∴ 
= 
，
∴DE=BF=6，
∵AH⊥BC，
∴CH=BH，
∵CA=AF，
∴AH为△CBF的中位线，
∴AH= 
BF=3．
∴BH= 
= 
=4，
∴BC=2BH=8．
故答案为：A．
作直径CF，连结BF，作AH⊥BC于H，首先依据等角的补角相等得到∠DAE=∠BAF，然后再根据同圆中，相等的圆心角所对的弦相等得到DE=BF=6，接下来，在Rt△BAH中，依据勾股定理可求得BH的长，然后依据垂径定理可得到BC=2BH.
练习册系列答案
科学实验活动册系列答案
相关题目
