题目内容
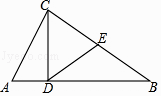
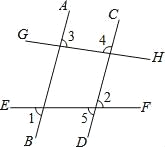
【题目】已知:如图,直线 AB,CD 被直线 EF,GH 所截,且∠1=∠2.求证:∠3+∠4=180°.
请将以下推理过程补充完整:
证明:∵直线 AB,CD 被直线 EF 所截,(已知)
∴∠2=∠5._____________
又∵∠1=∠2,(已知)
∴∠1=∠5,_______
∴_______∥_______,_______
∴∠3+∠4=180°._______.
【答案】对顶角相等 等量代换 AB CD 同位角相等,两直线平行 两直线平行,同旁内角互补
【解析】
根据平行线的性质和判定方法分别填空即可.
∵直线 AB,CD 被直线 EF 所截,(已知)
∴∠2=∠5.(对顶角相等)
又∵∠1=∠2,(已知)
∴∠1=∠5,(等量代换)
∴AB∥CD,(同位角相等,两直线平行)
∴∠3+∠4=180°.(两直线平行,同旁内角互补).
故答案为:对顶角相等,等量代换,AB∥CD,同位角相等,两直线平行,两直线平行,同旁内角互补

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A.众数是8
B.中位数是3
C.平均数是3
D.方差是0.34