题目内容
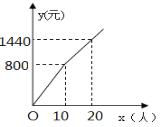
【题目】某旅游风景区，门票价格为a元/人，对团体票规定：10人以下(包括10人)不打折，10人以上超过10人部分打b折.设团体游客
人，门票费用为y元，y与x之间的函数关系如图所示.
(1)填空：a＝_______；b＝_________.
(2)请求出：当x＞10时，
与
之间的函数关系式；
(3)导游小王带A旅游团到该景区旅游，付门票费用2720元（导游不需购买门票），求A旅游团有多少人？
【答案】(1)80；8（2）y=64x+160；（3）40人
【解析】（1）根据函数图象可以求得a、b的值；
（2）根据函数图象可以求得当x＞10时，y与x之间的函数关系式；
（3）根据（2）中的解析式可以求得A旅游团的人数．
（1）由图象可知，
a=800÷10=80，
b=
×10=8，
故答案为：80，8；
（2）当x＞10时，设y与x之间的函数关系式是y=kx+m，
则
，
解得，
，
即当x＞10时，y与x之间的函数关系式是y=64x+160；
（3）∵2720＞800，
∴将y=2720代入y=64x+160，得
2720=64x+160，
解得，x=40，
即A旅游团有40人．
练习册系列答案
相关题目
