题目内容
若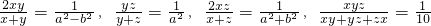
，则|a|=________．
2
分析：首先利用分式的基本性质化简得到（1）、（2）、（3）、（4），（1）+（2）+（3）得到和（4）类似的式子，将（4）代入即可求出a值．
解答：
=
，
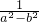即：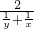
=，
∴
+
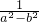=2a2-2b2（1），
同理：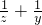
=a2（2），
+=2a2+2b2（3），
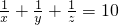（4），
（1）+（2）+（3）得：2（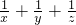
）=5a2（5），
把（4）代入（5）得：20=5a2，
解得：|a|=2．
故答案为：2．
点评：本题主要考查了分式的混合运算，分式的基本性质，解一元二次方程等知识点，能巧妙地变式是解此题的关键．
分析：首先利用分式的基本性质化简得到（1）、（2）、（3）、（4），（1）+（2）+（3）得到和（4）类似的式子，将（4）代入即可求出a值．
解答：
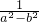=，即：
=，∴
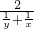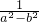+=2a2-2b2（1），同理：
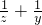=a2（2），+=2a2+2b2（3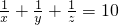），（4），（1）+（2）+（3）得：2（
）=5a2（5），把（4）代入（5）得：20=5a2，
解得：|a|=2．
故答案为：2．
点评：本题主要考查了分式的混合运算，分式的基本性质，解一元二次方程等知识点，能巧妙地变式是解此题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
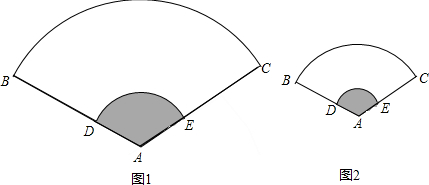角和半径．
如图所示，AB是⊙O的直径，弦CD与AB交于点E，若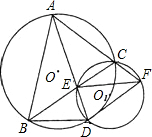
如图，已知△ABC三顶点在⊙O上，D为