题目内容
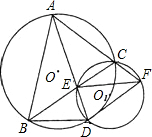 如图,已知△ABC三顶点在⊙O上,D为
如图,已知△ABC三顶点在⊙O上,D为 | BC |
(1)求证:∠BAD=∠DFE;
(2)求证:△AEC∽△FED;
(3)AB=AD是否成立?若成立则证明之,若不成立,则请你增加一个条件使其成立,并说明理由.
分析:(1)连接CD,根据等弧所对的圆周角相等得到∠BAD=∠BCD=∠EFD;
(2)根据等弧所对的圆周角相等得到∠CAE=∠BAD,结合(1)中的结论得到∠CAE=∠EFD,再根据圆内接四边形的性质得到∠ACE=∠FDE,从而证明三角形相似;
(3)能够根据结论分析探讨需要满足的条件,熟练运用圆周角定理的推论进行角之间的转换.
(2)根据等弧所对的圆周角相等得到∠CAE=∠BAD,结合(1)中的结论得到∠CAE=∠EFD,再根据圆内接四边形的性质得到∠ACE=∠FDE,从而证明三角形相似;
(3)能够根据结论分析探讨需要满足的条件,熟练运用圆周角定理的推论进行角之间的转换.
解答: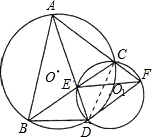 (1)证明:连接CD,
(1)证明:连接CD,
∵∠ABD=∠BCD,∠BCD=∠EFD,
∴∠BAD=∠EFD.
(2)证明:∵D为
的中点,
∴∠CAE=∠BAD.
∴∠CAE=∠EFD.
又∵∠AEC=∠EDF,
∴△ACE∽△FDE.
(3)解:由题设不足以说明AB=AD.
若AB=AD,则∠ABD=∠ADB,
由A、B、D、C四点在⊙O上知∠FCD=∠ABD,
又在⊙O1中,∠FCD=∠FED,∠FED=∠ADB,
只须增加条件∠FED=∠ADB,
即EF∥BD,
逆推之,即可证明AD=AB.
 (1)证明:连接CD,
(1)证明:连接CD,∵∠ABD=∠BCD,∠BCD=∠EFD,
∴∠BAD=∠EFD.
(2)证明:∵D为
 |
| BC |
∴∠CAE=∠BAD.
∴∠CAE=∠EFD.
又∵∠AEC=∠EDF,
∴△ACE∽△FDE.
(3)解:由题设不足以说明AB=AD.
若AB=AD,则∠ABD=∠ADB,
由A、B、D、C四点在⊙O上知∠FCD=∠ABD,
又在⊙O1中,∠FCD=∠FED,∠FED=∠ADB,
只须增加条件∠FED=∠ADB,
即EF∥BD,
逆推之,即可证明AD=AB.
点评:综合运用了圆周角定理推论、圆内接四边形的性质以及相似三角形的性质和判定.连接两圆的公共弦也是圆中常见的辅助线之一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
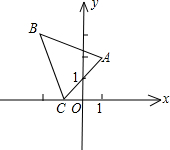 如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点A′,B′,C′.下列说法正确的是( )
如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点A′,B′,C′.下列说法正确的是( )| A、△A′B′C′与△ABC是位似图形,位似中心是点(1,0) | B、△A′B′C′与△ABC是位似图形,位似中心是点(0,0) | C、△A′B′C′与△ABC是相似图形,但不是位似图形 | D、△A′B′C′与△ABC不是相似图形 |
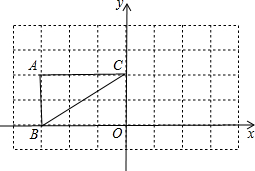 如图,已知△ABC三个顶点的坐标分别为:A(-3,2)、B(-3,0)、C(0,2),
如图,已知△ABC三个顶点的坐标分别为:A(-3,2)、B(-3,0)、C(0,2), 如图,已知△ABC三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0). 如图,已知△ABC三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0)
如图,已知△ABC三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0) 在平面直角坐标系中,如图,已知△ABC三个顶点的坐标分别为A(1,-4),B(5,-4),C(4,-1),
在平面直角坐标系中,如图,已知△ABC三个顶点的坐标分别为A(1,-4),B(5,-4),C(4,-1),