题目内容
【题目】如图,在ABCD中,E是CD的中点,AE是延长线交BC的延长线于F,分别连接AC,DF,解答下列问题: 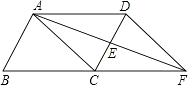
(1)求证:△ADE≌△FCE;
(2)若DC平分∠ADF,试确定四边形ACFD是什么特殊四边形?请说明理由.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠F,∠D=∠ECF,
又∵E是DC的中点,
∴DE=CE,
在△ADE和△FCE中, 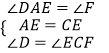 ,
,
∴△ADE≌△FCE(AAS)
(2)解:若DC平分∠ADF,则四边形ACFD是菱形;理由如下:
∵△ADE≌△FCE,
∴AD=CF,
又∵AD∥CF,
∴四边形ACFD是平行四边形,
∵DC平分∠ADF,
∴∠ADC=∠CDF,
∴∠FCD=∠CDF,
∴DF=CF,
∴四边形ACFD是菱形
【解析】(1)由平行四边形的性质和中点的性质,易得∠DAE=∠F,∠D=∠ECF,AE=CE,继而证得:△ADE≌△FCE.(2)由第(1)问中△ADE≌△FCE,易得AD=CF,又由AD∥CF,即可证得四边形ACFD是平行四边形,再证出DF=CF,即可得出结论.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).

练习册系列答案
相关题目




