题目内容
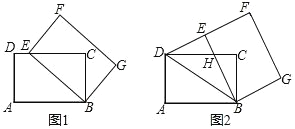
【题目】如图所示，平行四边形
中，点
在边
上，以
为折痕，将
向上翻折，点
正好落在
上的
处，若
的周长为8，
的周长为22，则
的长为__________．
【答案】7.
【解析】
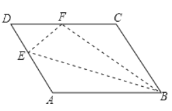
依据△FDE的周长为8，△FCB的周长为22，即可得出DF+AD=8，FC+CB+AB=22，进而得到平行四边形ABCD的周长=8+22=30，可得AB+BC=BF+BC=15，再根据△FCB的周长=FC+CB+BF=22，即可得到CF=22-15=7．
解：由折叠可得，EF=AE，BF=AB．
∵△FDE的周长为8，△FCB的周长为22，
∴DF+AD=8，FC+CB+AB=22，
∴平行四边形ABCD的周长=8+22=30，
∴AB+BC=BF+BC=15，
又∵△FCB的周长=FC+CB+BF=22，
∴CF=22-15=7，
故答案为：7.
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
