题目内容
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
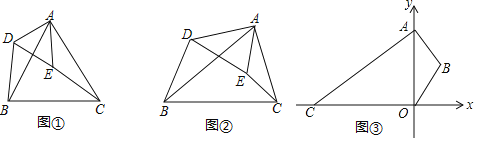
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
【答案】探究:见解析;应用:![]() .
.
【解析】
探究:由△DAE∽△BAC,推出![]() ,可得
,可得![]() ,由此即可解决问题;
,由此即可解决问题;
应用:当点D在AC的下方时,先判定△ABO∽△ADC,得出![]() ,再根据∠BAD=∠OAC,得出△ACO∽△ADB,进而得到∠ABD=∠AOC=90°,得到当OD⊥BE时,OD最小,最后过O作OF⊥BD于F,根据∠OBF=30°,求得OF=
,再根据∠BAD=∠OAC,得出△ACO∽△ADB,进而得到∠ABD=∠AOC=90°,得到当OD⊥BE时,OD最小,最后过O作OF⊥BD于F,根据∠OBF=30°,求得OF=![]() OB=
OB=![]() ,即OD最小值为
,即OD最小值为![]() ;当点D在AC的上方时,作B关于y轴的对称点B',则同理可得OD最小值为
;当点D在AC的上方时,作B关于y轴的对称点B',则同理可得OD最小值为![]() .
.
解:探究:如图②中,
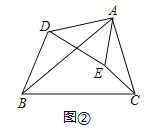
∵∠BAC=∠DAE,∠ABC=∠ADE,
∴△DAE∽△BAC,∠DAB=∠EAC,
∴![]() ,
,
∴![]() ,
,
∴△ABD∽△ACE;
应用:①当点D在AC的下方时,如图③1中,
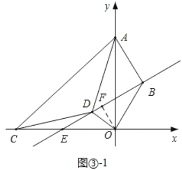
作直线BD,由∠DAC=∠DCA=∠BAO=∠BOA=30°,可得△ABO∽△ADC,
∴![]() ,即
,即![]() ,
,
又∵∠BAD=∠OAC,
∴△ACO∽△ADB,
∴∠ABD=∠AOC=90°,
∵当OD⊥BE时,OD最小,
过O作OF⊥BD于F,则△BOF为直角三角形,
∵A点的坐标是(0,6),AB=BO,∠ABO=120°,
∴易得OB=2![]() ,
,
∵∠ABO=120°,∠ABD=90°,
∴∠OBF=30°,
∴OF=![]() OB=
OB=![]() ,
,
![]() ;
;
当点D在AC的上方时,如图③2中,
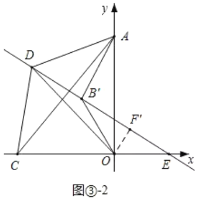
作B关于y轴的对称点B',作直线DB',则同理可得:△ACO∽△ADB',
∴∠AB'D=∠AOC=90°,
∴当OD⊥B'E时,OD最小,
过O作OF'⊥B'D于F',则△B'OF'为直角三角形,
∵A点的坐标是(0,6),AB'=B'O,∠AB'O=120°,
∴易得OB'=2![]() ,
,
∵∠AB'O=120°,∠AB'D=90°,
∴∠OB'F'=30°,
∴OF'=![]() OB'=
OB'=![]() ,
,
即OD最小值为![]() .
.
故答案为:![]() .
.