题目内容
【题目】如图,数轴上![]() ,
,![]() 两点对应的数分别为
两点对应的数分别为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 同时从原点出发,点
同时从原点出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴正方向运动,点
个单位长度的速度沿数轴正方向运动,点![]() 以每秒
以每秒![]() 个单位长度的速度先沿数轴负方向运动,到达点
个单位长度的速度先沿数轴负方向运动,到达点![]() 后再沿数轴正方向运动,当点
后再沿数轴正方向运动,当点![]() 到达点
到达点![]() 后,两个点同时结束运动.设运动时间为
后,两个点同时结束运动.设运动时间为![]() 秒.
秒.

(1)当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
(2)通过计算说明,当![]() 在不同范围内取值时,线段
在不同范围内取值时,线段![]() 的长度如何用含
的长度如何用含![]() 的式子表示?
的式子表示?
(3)当点![]() 是
是![]() 的中点时直接写出
的中点时直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)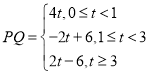 ;(3)当
;(3)当![]() 是
是![]() 的中点出现在第一阶段时,
的中点出现在第一阶段时, ![]() ;当
;当![]() 是
是![]() 的中点出现在第二阶段时,
的中点出现在第二阶段时, ![]() .
.
【解析】
(1)求得当![]() 时,点
时,点![]() 所在的位置之后再求线段
所在的位置之后再求线段![]() 的长度.
的长度.
(2)整个运动过程分成几个不同的阶段,第一阶段,![]() 两点反向相离,两点距离变大;第二阶段,当
两点反向相离,两点距离变大;第二阶段,当![]() 到达
到达![]() 点后变为追及问题,两者距离变小;第三阶段,当
点后变为追及问题,两者距离变小;第三阶段,当![]() 追上
追上![]() 之后继续运动,两者距离又变大.分别分析这三段过程的时间节点并用线段长度表示出
之后继续运动,两者距离又变大.分别分析这三段过程的时间节点并用线段长度表示出![]() 即可.
即可.
(3)点![]() 是
是![]() 的中点可以出现在运动的第一和第二阶段,分析数量关系代入即可.
的中点可以出现在运动的第一和第二阶段,分析数量关系代入即可.
解: (1)当![]() 时,
时,![]() 向右运动至点1处,
向右运动至点1处, ![]() 向左运动至-3处,
向左运动至-3处,
所以![]() .
.
(2)第一阶段,当![]() 时,
时, ![]() ;
;
第二阶段,![]() 追上
追上![]() 用时
用时![]() 秒,所以当
秒,所以当![]() 时,
时, ![]() ;
;
第三阶段, 第3秒时,![]() 超越
超越![]() ,所以当
,所以当![]() 时,
时, ![]() .
.
综上, 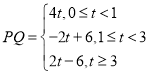 .
.
(3)当![]() 是
是![]() 的中点出现在第一阶段时,
的中点出现在第一阶段时,
由题意得![]() ,
,
![]()
解得![]() .
.
当![]() 是
是![]() 的中点出现在第二阶段时,
的中点出现在第二阶段时,
由题意得![]() ,
,
![]()
解得![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】小明与小红开展读书比赛.小明找出了一本以前已读完84页的古典名著打算继续往下读,小红上个周末恰好刚买了同一版本的这本名著,不过还没开始读.于是,两人开始了读书比赛.他们利用下表来记录了两人5天的读书进程.例如,第5天结束时,小明还领先小红24页,此时两人所读到位置的页码之和为424.已知两人各自每天所读页数相同.
读书天数 | 1 | 2 | 3 | 4 | 5 |
页码之差 | 72 | 60 | 48 | 36 | 24 |
页码之和 | 152 | 220 | 424 |
(1)表中空白部分从左到右2个数据依次为 , ;
(2)小明、小红每人每天各读多少页?
(3)已知这本名著有488页,问:从第6天起,小明至少平均每天要比原来多读几页,才能确保第10天结束时还不被小红超过?(答案取整数)