题目内容
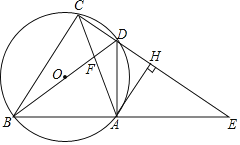
【题目】如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )
A.2![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
连接CF、FG,先证明△AFD∽△EAD,得出![]() ,结合DF=5EF,可计算出AD,AF的长,再证明△AFG∽△DFC,从而得出
,结合DF=5EF,可计算出AD,AF的长,再证明△AFG∽△DFC,从而得出![]() ,求出AG,即可由DG=AD-AG解题.
,求出AG,即可由DG=AD-AG解题.
解:连接CF、FG,
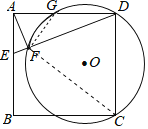
∵正方形ABCD中,∠EAD=∠ADC=90°,AF⊥DE,
∴∠AFD=∠EAD=90°,又∠ADF=∠EDA,
∴△AFD∽△EAD,
∴![]() ,
,
又∵DF=5EF=5,∴EF=1,ED=6,
∴AD=![]() ,
,
在Rt△AFD中,AF=![]() =
=![]() ,
,
∵∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,
∴∠DAF=∠CDF,
∵四边形GFCD是⊙O的内接四边形,
∴∠FCD+∠DGF=180°,
∵∠FGA+∠DGF=180°,
∴∠FGA=∠FCD,
∴△AFG∽△DFC.
∴![]() ,
,
∴![]() ,
,
∴AG=![]() ,
,
∴DG=AD﹣AG=![]() ,
,
故选:D.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目