题目内容
【题目】如图,在等边△ABC中,AB=BC=AC=6cm,点P从点B出发,沿B→C方向以1.5cm/s的速度运动到点C停止,同时点Q从点A出发,沿A→B方向以1cm/s的速度运动,当点P停止运动时,点Q也随之停止运动,连接PQ,过点P作BC的垂线,过点Q作BC的平行线,两直线相交于点M.设点P的运动时间为x(s),△MPQ与△ABC重叠部分的面积为y(cm2)(规定:线段是面积为0的图形).
(1)当x= (s)时,PQ⊥BC;
(2)当点M落在AC边上时,x= (s);
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
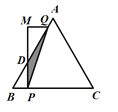
【答案】(1)1.5;(2)3;(3)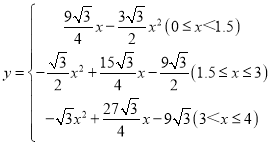
【解析】
(1)令PQ⊥BC,表示出BP和BQ的长,利用余弦的定义得出方程,求解即可;
(2)根据△ABC是等边三角形得出BQ=CM,表示出PC的长,结合余弦的定义得出方程,求解即可;
(3)根据(1)和(2)中结论,分0≤x<1.5时,1.5≤x≤3时,3<x≤4时三种情况画出图形,求出相应边长,可得函数解析式.
解:(1)当PQ⊥BC时,
BP=1.5x,BQ=6-x,
∴BQ=![]() ,即6-x=
,即6-x=![]() ,
,
∴6-x=3x,
解得:x=1.5,
∴当x=1.5时,PQ⊥BC;
(2)∵△ABC是等边三角形,QM∥BC,
∴AQ=AM,BQ=CM,
PC=6-1.5x,CM=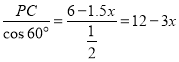 ,
,
∴BQ=12-3x,AQ=x,
∴12-3x+x=6,
解得x=3,
∴当点M落在AC上时,x=3(s);
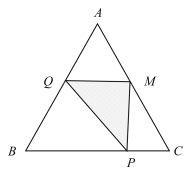
(3)当0≤x<1.5时,过Q作QE⊥BC于E,
∵BQ=6-x,
∴QE=BQsin∠B=BQsin60°,而DP=BPtan∠B=BPtan60°,
y=S△BPQ-S△BPD
=![]()
=![]()
=![]() ;
;
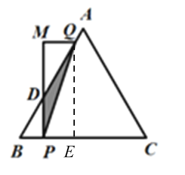
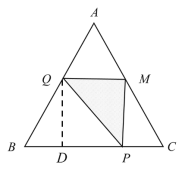
当1.5≤x≤3时,过点Q作QD⊥BC于D,
可知:四边形QDPM为矩形,
∴QM=DP=BP-BD=BP-BQ·cos60°,
PM=MC·sin60°=BQ·sin60°,
则y=S△PQM
=![]()
=![]()
=![]() ;
;
当3<x≤4时,
如图所示,过点Q作QE⊥BC于点E,
可知四边形QEPM为矩形,
∴QM=EP=BP-BE=BP-BQ·tan∠B=1.5x-![]() (6-x)=2x-3,
(6-x)=2x-3,
∵QM∥BC,
∴△AQO为等边三角形,∠MON=∠C=60°,
∴AQ=OQ=AO=x,
∴OM=QM-OQ=2x-3-x=x-3,
∵PC=6-1.5x,∠C=60°,
∴NP=PC·tan∠C= PC·tan60°=![]() ,
,
∴MN=MP-NP=QE-NP=BQ·sin∠B-NP=(6-x)·sin60°-![]() =
=![]() ,
,
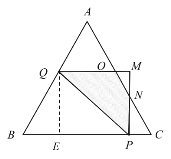
y=S△PQM-S△NOM
=![]()
=![]() -
-![]() (x-3)(
(x-3)(![]() )
)
=![]()
故y关于x的函数解析式为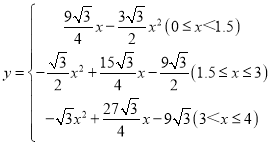 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案