Question

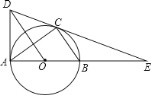
【题目】如图，⊙O是△ABC的外接圆，AB是直径，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．(1)、求证：DE是⊙O的切线；(2)、若AE=6，CE=,求线段CE、BE与劣弧BC所围成的图形面积.（结果保留根号和π）

Answer 1

【答案】(1)、证明过程见解析；(2)、2.

【解析】

试题分析：(1)、连接OC得出∠AOD=∠COD，证明△AOD和△COD全等得出切线；(2)、根据Rt△OCE的勾股定理求出半径，然后得出∠COE的度数，然后求出扇形COB的面积，从而得出所求图形的面积.

试题解析：(1)、连结OC，证得∠AOD=∠COD ；证得△AOD≌△COD（SAS）； 证得∠OCD=∠OAD=90°；

则DE是⊙O的切线.

(2)、设半径为r，在Rt△OCE中，OC2+CE2=OE2 解得

所求图形面积为